王军峰1,徐越群1,蔡承才2
1.石家庄铁路职业技术学院,河北 石家庄 050061;2.石家庄铁道大学,河北 石家庄 050043
摘 要:塑料薄膜制造中吹塑机的张力控制是决定塑料薄膜厚度、强度和质量的一个重要因素。针对吹塑机的张力控制系统的一阶积分时滞模型,提出一种新的基于MDP方法的PID控制器。基于一个假设,即多主导极是正的、稳定的,并且过程控制系统无振荡,同时需要假设非主导的极点或者零点对控制过程的影响不显著。为了提高伺服性能,降低超调量,在PID控制结构中使用了设定点权重参数。控制过程简洁,控制器参数以表达式的形式给出。仿真案例实验结果表明,设计具有良好的追踪性能和调节性能,并且鲁棒性良好,适用于张力控制。
关键词:吹塑机;张力控制;PID控制器;MDP;设定点权重参数
塑料薄膜在我国的产量约占全部塑料制品产量的20%,同时塑料薄膜的生产量增涨速度在所有塑料制品中最快[1],各行各业对塑料薄膜的需求量也在逐年增长[2]。塑料薄膜应用范围十分广泛,涉及农 业[3]、工业[4]、商业以及人们日常生活中的方方面面[5]。
塑料薄膜在制造过程中,首先需要把塑料材料加热熔融,使用各种方法将其塑造成膜状[6]。这些方法包括压延法[7]、拉伸法[8]和吹塑法[9]。其中吹塑法需要将塑料熔融材料进行纵向和横向的双向拉伸,因此制造出的塑料薄膜强度较好,是应用最广泛的塑料薄膜成型方 法[10-11]。
在吹塑机的工作过程中,最关键的技术就是其张力控制系统的控制[12],它决定了塑料薄膜产品的厚度、均匀程度、强度和品质[13]。目前,国内的大中型塑料薄膜生产制造商使用的吹塑机大多依赖进口[14]。因此针对塑料薄膜制造研究吹塑机的张力控制意义重大。
目前工业中大多采用PID控制结构,吹塑机的张力控制也是如 此[15]。PID控制器不仅能够通过合理设计提高张力控制精度,其较强的扰动抑制性也能使得吹塑机在电磁扰动等各种扰动情况下依旧维持稳定运行[16]。目前,各种文献中记载了很多种关于设计PID控制器的方法,如直接综合法[17]、Z-N法[18]、频域法[19]、实证法[20]、内模控制法[21]、等值系数法[22]、二自由度控制法[23-24]、稳定分析法[25]和各种最优化算法[26-27]等。这些方法具有一定的优点,比如直接综合法设计过程简单明了、计算量少,但是对于扰动性能的提高有一定局限性[28];Z-N法是最经典的方法,操作简单,但是性能较差[29];内模控制法虽然性能优良,但是计算过程较为繁复,使用条件较为苛刻,普适性较差;最优算法编程复杂,且存在大量迭代和模拟验证过程。
本研究针对塑料薄膜生产中的吹塑机的张力控制系统,提出一 种新的基于MDP(Multiple Dominant Pole-placement)的PID控制器的设计方法。这种方法基于一个假设,即存在多主导极点,并且其是正的、稳定的,过程控制无振荡。同时,需要假设非主导的极点或者零点对控制过程的影响不显著。这种方法过程简洁,控制器参数将以表达式的形式给出,控制效果良好,适用于张力控制系统的设计。
01 方法设计
1.1 PID控制结构的设计
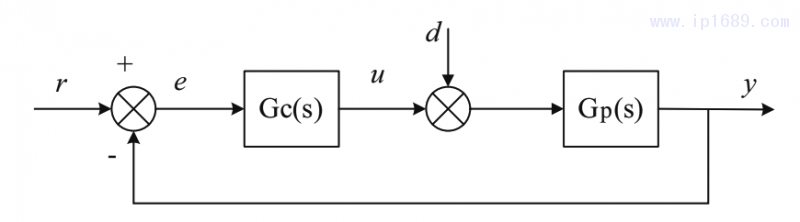
图1为所设计的PID控制结构。
图1中,r为期望变量;e为控制误差;u为操纵变量;d为扰动量;y为被控变量;Gc(s)为PID控制器;Gp(s)为过程系统模型。
多主导极点S*p + 1 可以通过式(1)得到:
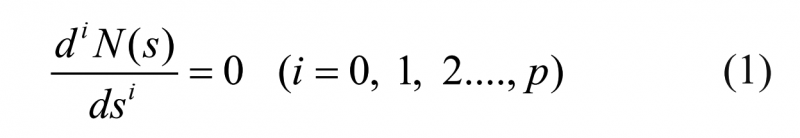
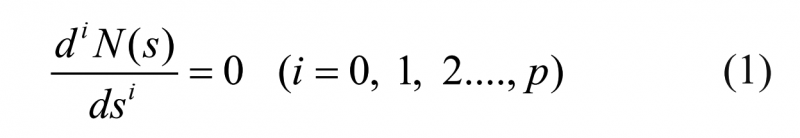
式(1)中:N(s)为针对有时滞的或者没有时滞的过程系统与PID控制器组成的闭环控制系统特征拟多项式;p为控制器的可调整参数的数量。
图1中的过程系统模型Gp(s) 将由式(2)表示:
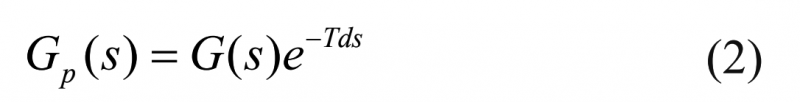
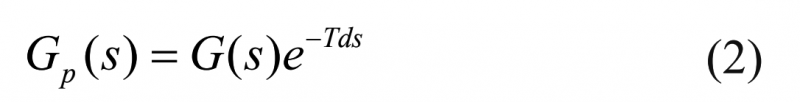
吹塑机的张力控制系统属于一阶积分系统,将式(2)细化为式(3):
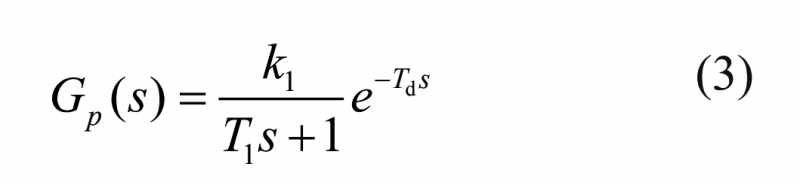
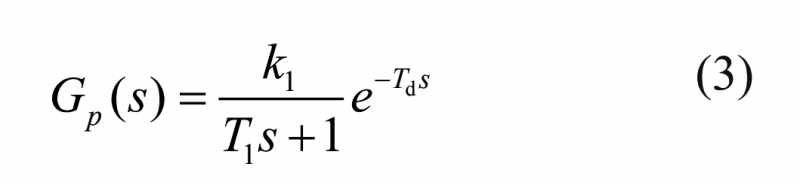
PID控制器的传递函数为:
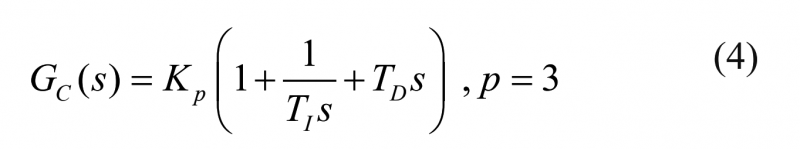
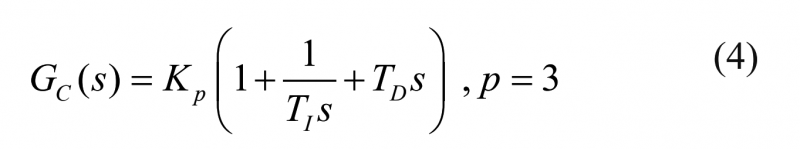
式中:G (s)为过程传递函数去掉时滞的部分;kc为控制器增益;TI为积分时间;TD为微分时间;Kp为控制器增益;Td为过程滞后时间。
1.2 基于MDP方法的PID控制算法
根据系统方程(1)的过程系统方程(2)和标准PID控制器(4),可以得到四重主导极点S*4和3个可调整参数K*P,T*I,T*D, 过程系统(2)的近似系统传递函数和标准PID控制器(4)将通过MDP方法调整为:
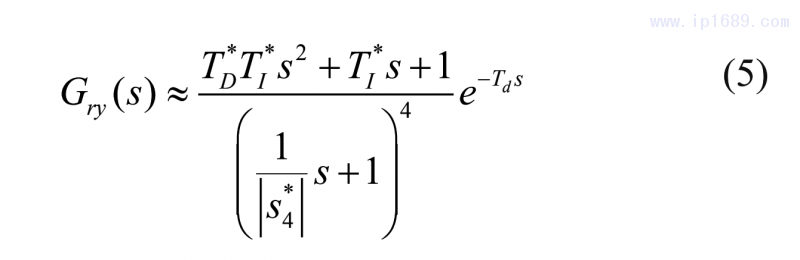
式(5)中的拟多项式是Hurwitz多项式,它的零点加速了瞬态过程并且产生了伺服响应中不被许可的过大超调量,对于标准的PID控制器,假设式(5)的相等关系恒定,当出现下面不平等关系时,超调量将出现:
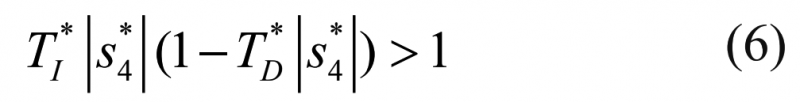
对于积分系统式(6)的不平等关系将一直成立,因此伺服响应中的超调量不能被移除。事实上,标准的PID控制器在控制积分系统时,不能实现没有超调量的伺服响应也许能以另一种方式实现。
标准PID控制器和积分过程系统组成的闭环系统的控制误差,在期望输入变量 r(t) =r0的作用下将表示为:
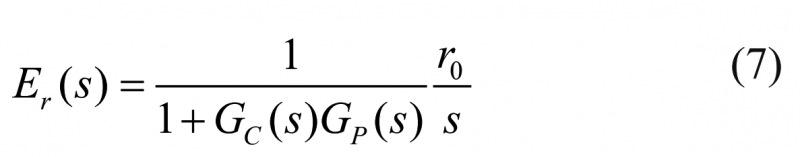
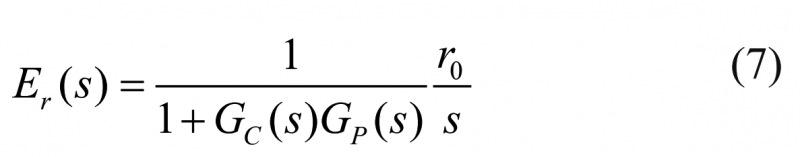
因为在控制区域它将成立以下关系:
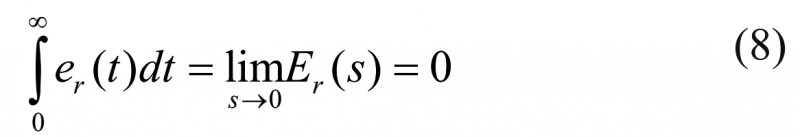
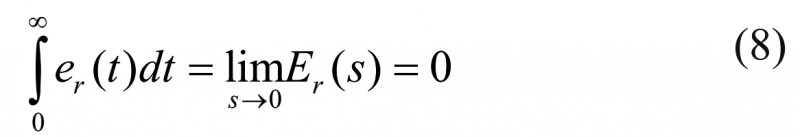
显然,伺服响应无法实现无超调量。对式(8)解释如下:伺服响应超过和低于r(t) =r0的中线区域是相等的。这个结论不仅对于MDP方法设计的控制系统,还广泛适用于所有的积分系统。因此考虑在输入信号后面加入设定点权重参数,以减小超调量并加快响应速度。
Arbogast等[30]和Begum等[31]使用了设定点权重参数,这样使得闭环传递函数零点从虚轴移除并且减少了超调量和稳定时间。ε作为设定点权重参数,在选择它时要求闭环系统响应没有超调和设置时间并且响应曲线是平滑的。因此ε应该设定在0~1这个范围之内。一般来说ε值大(接近于1),在设定点响应的时候会产生很大的超调量,而ε值小的时候,系统响应会变慢。Begum等[31]中经过大量的仿真研究提出,常规设定点权重参数ε=0.4时效果最佳。区别于常规PID,本研究将设定点权重参数设为ε=0.5以提高追踪性能。
表1为通过MDP方法计算得到的PID的可调整参数。表1为通过MDP方法计算得到的PID的可调整参数。

02 实例仿真
进行了一个由吹塑机张力控制系统一阶积分时滞系统模型来进行PID控制器的设计:
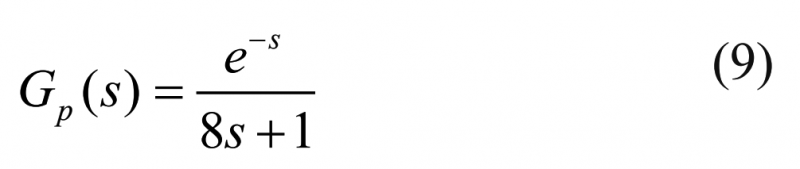
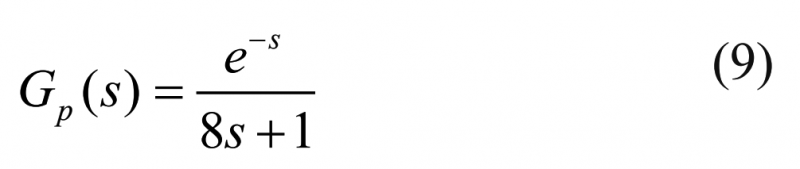
据MDP方法计算得到的参数为:
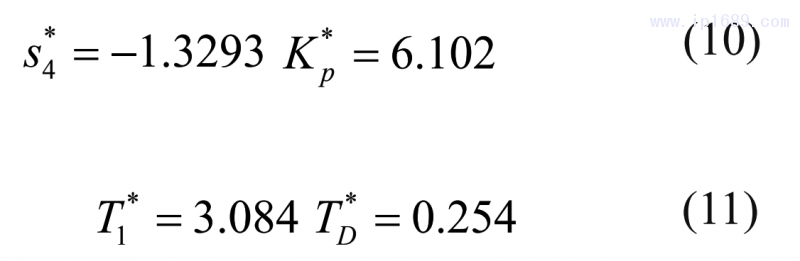
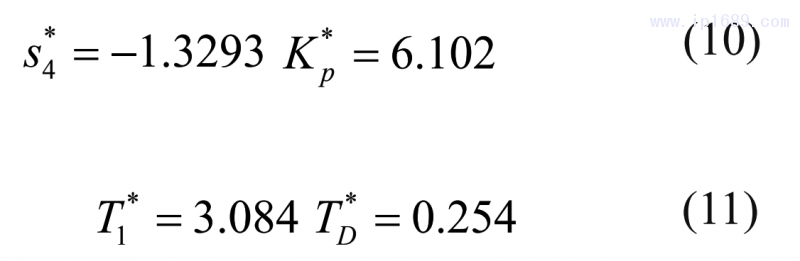
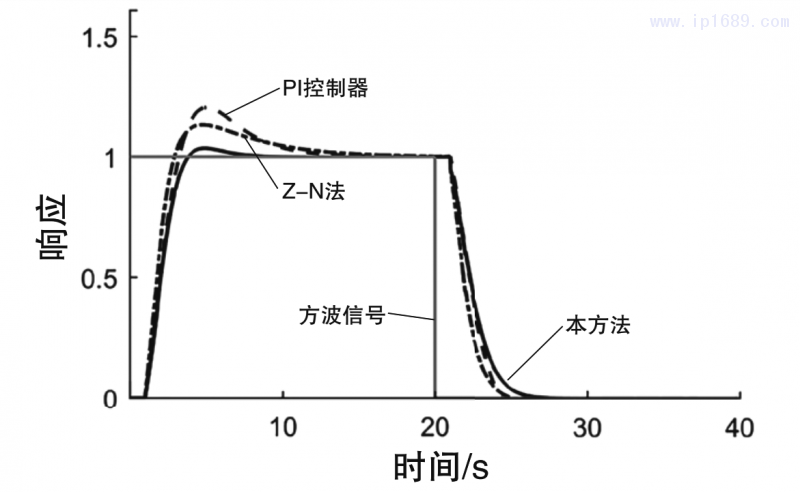
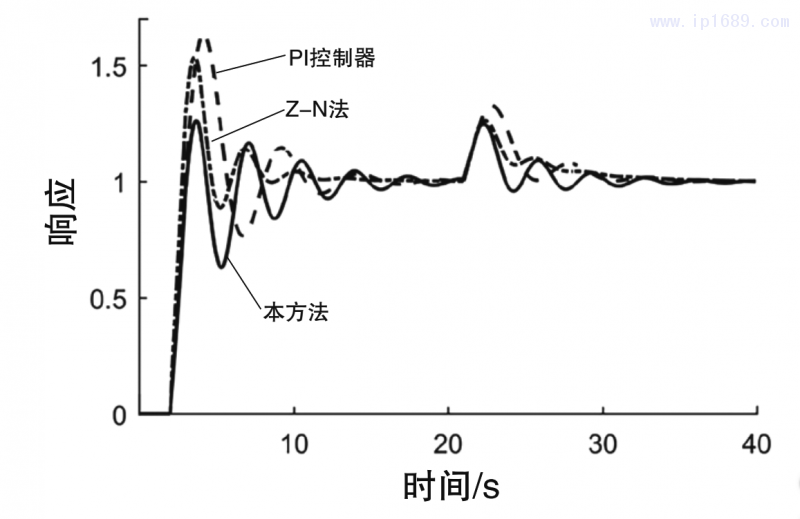
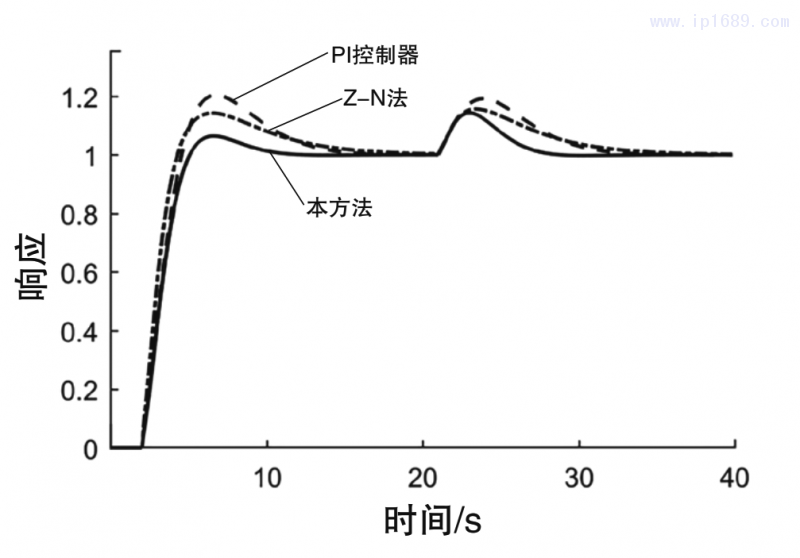
图2为所有对比方法的伺服响应和调节响应图;图3为闭环系统的方波响应图;图4为在时间常数k1过程系统模型比例常数由1变为2时的闭环响应曲线图,即失配情形1;图5为在时滞参数Td由1变为1.4时的闭环响应曲线图,即失配情形2;图6为在时间参数T1由8变为9时的闭环响应曲线图,即失配情形3。
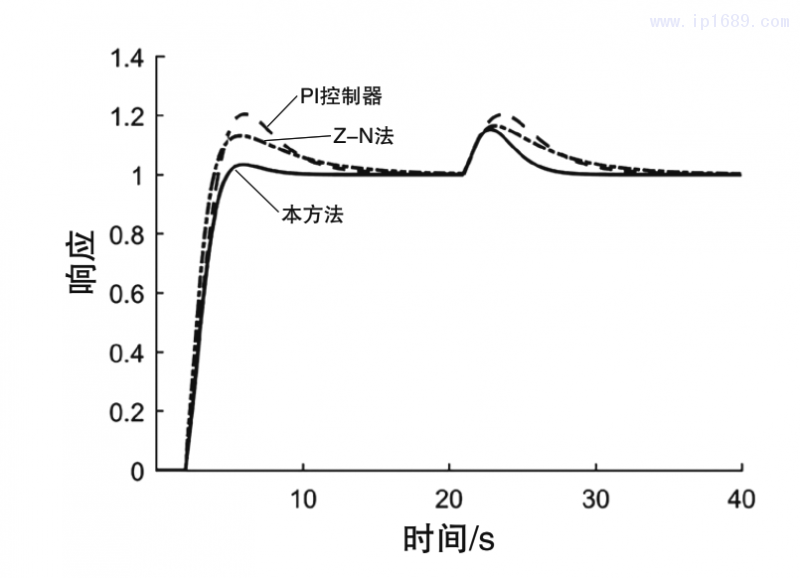
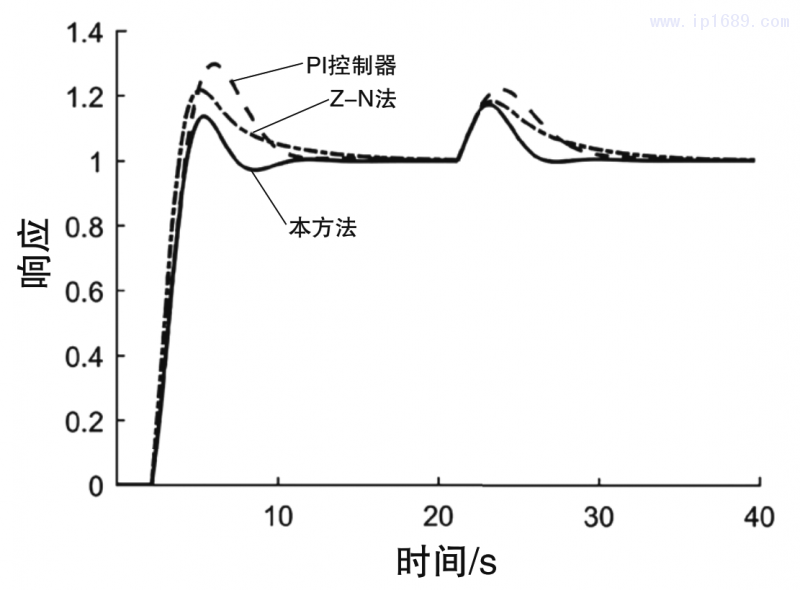
从图2可以看出,相比于PI控制器和使用Z-N法的PID控制器,本研究所采用的方法的伺服性能和扰动抑制性能最好,同时具有快速的上升时间和最小的超调量。相反PI控制器所在闭环系统的伺服响应最大的超调量,同时其扰动性能最差。使用Z-N法的PID控制器同样具有较差的调节性能,其伺服性能比PI控制器的稍微好一些。
由图3的方波响应图可以观察到,本研究所采用的方法在跟随给定信号的能力方面均优于常规PI控制器和使用Z-N法整定参数的PID控制器。
图4、图5和图6均给过程模型增加不同的摄动,以观察各种控制器在系统模型失配的情形下响应效果,可以看出即使在系统参数不稳定的情形下,本研究所采用的方法依旧表现出最佳的伺服性能和扰动抑制性能及良好的鲁棒性能。
3 结论
本研究探讨了塑料薄膜生产中的吹塑机的张力控制系统的鲁棒控制,在现有文献研究的基础上,提出了一种新的基于MDP方法的PID控制器的设计方法。基于一个假设,即存在一个稳定的实主导极点并且过程控制结构是无振荡的。同时,需要假设非主导的极点或者零点对控制过程的影响不显著。为了得到多主极点和PID控制器的可调参数,利用Matlab求解多组特征方程对s的各阶导数而组成的联立方程组。在吹塑机的张力控制系统的一阶积分时滞系统下进行了仿真实验,结果表明,本方法具有良好的追踪性能和调节性能,并且鲁棒性较好,非常适用于张力控制系统的设计。后续研究中将考虑使用优化算法,比如粒子群算法,遗传算法等结合多主导极点控制方法,使得所得到的控制器性能更加良好,此外将添加更多的优化目标,使得所设计的控制器更加适用于张力控制系统。
参考文献
[1] 傅明华,汪羞德,顾仲兰,等. 多功能转光塑料薄膜应用效应研究[J]. 农业工程学报,2000, 16(6): 81-84.
[2] 窦思红,谢兰桂,赵霞,等. 测量塑料薄膜氧气透过量的不确定度评定[J]. 塑料, 2018(3): 72-75.
[3] 黄身岐,林本农,唐健玲. 可控光、生物降解塑料薄膜工业化生产及应用研究[J]. 福建轻纺,2003(11): 1-9.
[4] 赵海丽,徐婉琪,杨元秀. 塑料薄膜在农业生产中的应用现状、问题、前景[J]. 南方农业,2014(15): 36-37.
[5] 王欣,王克俭. 农用大棚塑料薄膜材料发展综述[J]. 塑料包装, 2019(3): 22-31.
[6] 王盛楠,王亦红. 基于塑料薄膜疵点检测的生产设备故障诊断[J]. 机械制造与自动化, 2013, 42(2): 54-56.
[7] 孟新宇. 塑料薄膜压延过程的计算机仿真系统设计研究[J]. 塑料工业, 2016,44(3): 96-127.
[8] 罗海. 聚乙烯生产工艺技术探讨[J]. 绿色环保建材, 2019(8): 31-37.
[9] 姚畅. 塑料瓶新型吹瓶设备结构设计[J]. 内江科技, 2018, 39(1): 44-51.
[10] 刘军强. 多层中空吹塑机头的技术进展及创新[J]. 塑料包装, 2017, 27(5): 15-20.
[11] 杜巧连,陈卫增,俞鸿斌. 吹塑机型坯壁厚控制系统的优化设计[J]. 液压与气动, 2005(10): 64-66.
[12] 张航. PLC在全自动吹塑机电气控制系统中的应用[J]. 广东石油化工学院学报, 2009,19(6): 33-36.
[13] 黄虹,李子平. 吹塑机自动风环原理及应用[J]. 塑料包装, 2005(5): 40-41, 35.
[14] 张航,邓昌奇. 基于PLCN:N网络的模内贴标吹塑机控制系统设计[J].机床与液压,2012, 40(14): 101-103.
[15] 王安,李晓娟. BP神经网络PID控制在吹塑机系统中的应用[J]. 计算机仿真,2010(9): 161-164, 180.
[16] 吴宏鑫,沈少萍. PID控制的应用与理论依据[J]. 控制工程, 2003(1): 39-44.
[17] 景微娜,左信. 几种PID控制器设计方法的比较[J]. 计算机仿真, 2008,25(1): 270-273.
[18] 陈永庆. 基于Z-N算法的PID炉温控制[J]. 大连交通大学学报,2008(2): 43-50.
[19] 王冰,方跃法. PID控制器设计的频域性能图谱法[J]. 控制工程, 2018, 25(11): 1 953-1 958.
[20] 张晓路,于全训. 用于不稳定系统的PID调节法[J]. 山东建筑工程学院学报,2000,15(2): 51-55.
[21] 刘红军,韩璞,孙海蓉,等. 基于内模控制的PID控制器的设计[J]. 计算机仿真, 2005,22(3): 207-210.
[22] 孙德敏,杨彬彦. 相关系数辨识法PID自动整定软件及其工业应用[J].中国科学技术大学学报, 1995,25(4): 425-430.
[23] 姜金华,陈永良. 基于PID算法的二自由度自调节测高系统设计[J]. 自动化仪表, 2017,38(12): 17-23.
[24] 杨延西,刘丁. 基于模糊遗传算法的二自由度PID控制器优化设计[J].仪器仪表学报, 2006(8): 50-54.
[25] 欧林林,张卫东,顾诞英. PID控制作用下一阶时滞系统的鲁棒稳定性分析[J]. 上海交通大学学报,2006(11): 100-104.
[26] 蒋龙,施卫,王浩, 等. 基于遗传算法优化的无刷电机控制系统设计[J].电子制作,2019(17): 23-26.
[27] 穆海芳,韩君,李明. 改进的粒子群算法在磨煤机PID神经网络控制中的应用[J]. 金陵科技学院学报, 2019(2): 16-20.
[28] 邱丽,曾贵娥,朱学峰,等.几种PID控制器参数整定方法的比较研究[J]. 自动化技术与应用,2005(11): 31-34.
[29] 刘喆,李杰,刘俊,等. 改进型Z-N参数整定方法及其硬件实现[J]. 科技通报,2012(2): 109-111.
[30] Arbogast J E, Cooper D J. Extension of IMC tuning correlations for non-self regulating (integrating) processes[J]. ISA Transactions, 2007, 46(3): 303-311.
[31] Begum K G,Rao A S,Radhakrishnan T K. Maximum sensitivity based analytical tuning rules for PID controllers for unstable dead time processes[J]. Chemical Engineering Research and Design, 2016, 109: 593-606.
[22] 孙德敏,杨彬彦. 相关系数辨识法PID自动整定软件及其工业应用[J].中国科学技术大学学报, 1995,25(4): 425-430.
[23] 姜金华,陈永良. 基于PID算法的二自由度自调节测高系统设计[J]. 自动化仪表, 2017,38(12): 17-23.
[24] 杨延西,刘丁. 基于模糊遗传算法的二自由度PID控制器优化设计[J].仪器仪表学报, 2006(8): 50-54.
[25] 欧林林,张卫东,顾诞英. PID控制作用下一阶时滞系统的鲁棒稳定性分析[J]. 上海交通大学学报,2006(11): 100-104.
[26] 蒋龙,施卫,王浩, 等. 基于遗传算法优化的无刷电机控制系统设计[J].电子制作,2019(17): 23-26.
[27] 穆海芳,韩君,李明. 改进的粒子群算法在磨煤机PID神经网络控制中的应用[J]. 金陵科技学院学报, 2019(2): 16-20.
[28] 邱丽,曾贵娥,朱学峰,等.几种PID控制器参数整定方法的比较研究[J]. 自动化技术与应用,2005(11): 31-34.
[29] 刘喆,李杰,刘俊,等. 改进型Z-N参数整定方法及其硬件实现[J]. 科技通报,2012(2): 109-111.
[30] Arbogast J E, Cooper D J. Extension of IMC tuning correlations for non-self regulating (integrating) processes[J]. ISA Transactions, 2007, 46(3): 303-311.
[31] Begum K G,Rao A S,Radhakrishnan T K. Maximum sensitivity based analytical tuning rules for PID controllers for unstable dead time processes[J]. Chemical Engineering Research and Design, 2016, 109: 593-606.












 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...














