黄雪梅 1,柳和生 1,2,黄兴元 1,黄益宾 3,余忠 3,江诗雨 1
(1. 南昌大学先进制造学院,南昌 330031 ; 2. 华东交通大学机电与车辆工程学院,南昌 330013 ;
3. 上饶师范学院物理与电子信息学院,江西省塑料制备成型重点实验室,江西上饶 334001)
摘要:应用 Polyflow软件构建模型;截取口模内30mm、口模外50mm的熔体,模拟不同入口流率和不同开口臂长对U型挤出制件拐角处剪切速率和X,Y,Z向流动速度的影响,应用Origin后处理软件对相关数据进行分析。研究表明,U型制件挤出时,U型件拐角处靠近口模壁的剪切速率远大于中心位置的剪切速率,入口流率越大或臂长越短,其对应的剪切速率越大,在口模内同一流线上的剪切速率基本是定值,但在口模出口接近5mm 处会迅速降低;U型件靠近口模壁处的X,Y,Z向流动速度和靠近中心线位置的X,Y 向速度,在口模内起始25mm的距离内为0,但在口模出口接近5mm左右,速度会剧变,入口流率越大和开口臂长越短,变化越剧烈,其中靠近口模壁的最后5mm的X向流动速度指向负方向,Y向流动速度指向正方向;而靠近截面中心线处最后5mm的速度方向先正后负,入口流率越大或臂长越短,Y向流动速度在出口处的变化越剧烈;靠近U型截面中心线的熔体的Z向流动速度在口模内起始25mm段距离内较均匀,在最后5mm开始慢慢降低。
关键词:挤出成型; 开口臂尺寸; U 型件;拐角
随着社会的飞速发展,工业用型材的需求越来越多,在人们的生产、生活及科研应用中,各类塑料异型挤出制件的应用也越来越多。但异型材的挤出成型过程比较复杂,难于得到理想的形状和尺寸,近年来,不断有专家学者对异型材挤出开展了不同的研究 [1-6]。柳和生等 [7] 基于流率平衡提出了橡胶材质的异型材挤出口模的设计方法。张广冬等[8]对传统的聚合物挤出成型的模流系数进行了修正,并进行了数值验证,蒋标等[9]根据硬质聚氯乙烯 (PVC-U) 熔体特性,引入了拉比诺维茨修正的哈根-伯肃叶公式计算公式,对模头内熔体压力影响因素进行了分析和检测对比。郭凯 [10] 针对异型材挤出口模设计效率、自动化程度低,结合 UG/Open二次开发、UDO关联技术及MFC技术开发了塑料异型材挤出定型模系统并进行了验证。柳和生等[11]采用PPT黏弹模型对T异型材挤出口模内黏弹流动进行研究,模拟发现,在口模出口处流动速度、剪切 速率、压力、应力分布剧变,应力易集中发生在口模截面的拐角处。杨佳黎等[12]运用Polyflow逆向挤出功能对T型材变形倾向进行预测,在此基础上对T型材挤出口模进行了设计。Rutgers等[13]采用线型低密度聚乙烯研究了不同通道几何形状及壁面条件对挤出制件表面不稳定性的影响。Sienz等[14]利用有限元程序中的微分法进行敏感度分析,并尝试以压力降、平均切向流动速度及热传导等参数为性能指标并进行了模具设计。
综上所述,异型材难于成型在于其形状复杂,有很多拐角,其流动速度很不均匀,受型材拐角处的影响很大。笔者从熔体入口流率和U型件的开口臂尺寸两个方面来探讨其对拐角处挤出成型过程的影响。
1 理论模型
1.1 几何模型和有限元模型
以一种U形件为研究对象,该U型件截面如图1所示,相应的U型件截面参数见表1,其中B为U型件宽度,H为开口臂长,t为壁厚,Y为重心 距下底面的距离。应用Polyflow软件,以U型件开口方向中轴线为Y轴正向,U型件底部最下边缘线指向右为X轴正向,以右手笛卡尔直角坐标系确定Z轴正向,构建模型,截取口模内30mm、口模外50mm的熔体来进行研究。U型件的三维图及网格划分和边界设置如图2所示,各模型对应的网格数见表1。

图 1 U 型件截面

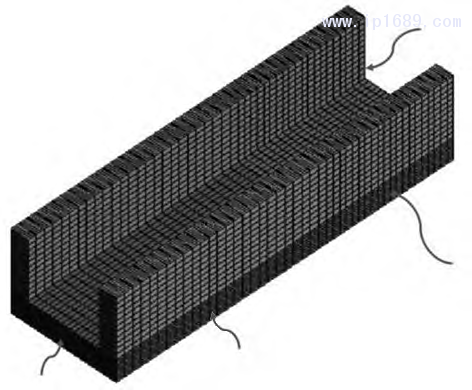
a—三维图;b—网格划分
图 2 口模内外所截取熔体的三维图及其网格划分
1.2 基本假设和基本方程
假设熔体都是不可压缩的,视整个流动过程为层流,在流动过程中忽略惯性力和质量力的作用。熔体为黏性流体。在假设成立的情况下,聚合物挤出成型过程中的流动满足聚合物流变学中的连续方程、动量方程及能量方程[15-16],微分黏弹本构模型选用Phan-Thien-Tanner (PTT) 本构模型[17],方程如式(1) 所示:
exp[tr(T1 )]T1 + λ[(1 - ) + ] = (1)
2(1 - ηr )η0 D
式中:ε——与熔体拉伸特性有关的材料参数;
λ——熔体松弛时间;
ηr——黏度比, ηr=η 1/η0,其中, η 1 为熔体零剪 切黏度中的黏性分量;
η0——熔体的零剪切黏度;
T1——偏应力张量;
ξ——与熔体剪切黏度有关的材料参数;
▽
T1 ——偏应力张量上熔体的上随体导数; 1 ——偏应力张量上熔体的下随体导数;
D——形变速率张量。
1.3 材料物性参数
在数值模拟中,采用的聚合物是熔体密度为973kg/m3的聚丙烯 (PP)。
1.4 边界条件设置
熔体入口流率分别为5×10-5,5×10-4,1×10-3, 5×10-3m3/s。
熔体与口模壁采用的是无滑移边界条件,此处与口模壁相邻边界表面上熔体的法向速度和切向速度都为0。
自由表面设置为free surface,指定自由表面的入口和出口,采用迎风面算法保持其计算的收敛。
在出口位置,熔体末端未施加任何牵引力,此处与口模壁相邻熔体边界上熔体的法向应力和切向速度都为0。
2 结果与讨论
先构造6个平面,坐标分布为Z=20,25,29,31,35,45mm 。平面1在口模内离口模出口10mm,平面2在口模内离口模出口5mm,平面3在口模内离口模出口1mm,平面4在口模外离口模出口1mm,平面5在口模外离口模出口5mm,平面6在口模外离口模出口15mm,通过模拟得到入口流率为1×10-3m3/s 时,6个平面上熔体的剪切速率和流动速度如图3所示。
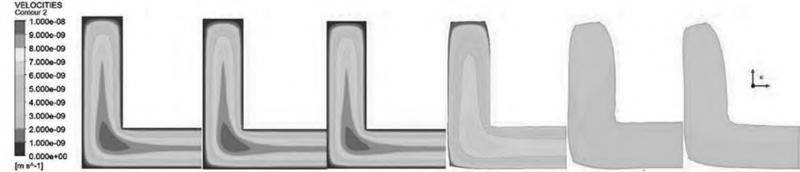

图 3 入口流率为 1 × 10-3 m3 时 6 个平面上熔体的剪切速率和流动流动速度
从图3可以发现:
(1) 口模出口外凸点拐角处熔体的剪切速率无变化,均为0。
(2) 在内拐角处熔体的剪切速率变化较大,故建立直线L1,其坐标为 (0.008 5,0.00 4,0) 和 (0.008 5,0.00 4,0.03),如图4所示。
(3) 同样,发现在两个拐角的中间熔体的流动速度最大,故在此位置也设置一条直线L2,其坐标为(0.010 5,0.002,0)和(0.010 5,0.002,0.03),如图4所示。
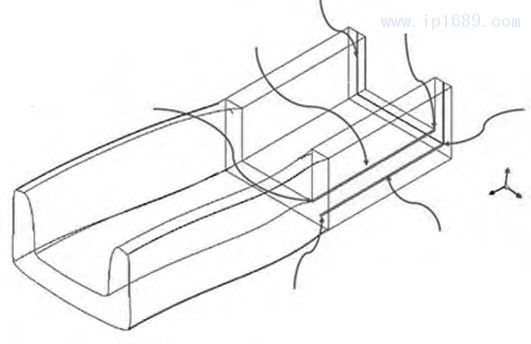
图 4 构建的直线 L1 和 L2
为了研究不同入口流率、不同开口臂长对熔体流动中剪切速率和流动速度的影响,选用4种不同入口流率 (5×10-5,5×10-4,1×10-3,5×10-3m3/s) 和4种不同开口臂长 (见表1) 分别对U型件进行模拟,然后应用Origin后处理软件对相关数据进行分析。
2.1 剪切速率分析
在开口臂长为15mm 条件下,入口流率不同时,直线L1和L2上熔体的剪切速率如图5所示。从图5可以看出,入口流率越大,直线L1和L2上熔体的剪切速率越大,并且在口模内起始25mm的一段距离内,同一流线上熔体的剪切速率基本是定值,仅在出口前大概5mm后,熔体的剪切速率急剧变小。对比图5a和图5b可以发现,U型槽拐角处靠近口模壁的剪切速率远大于中心位置的剪切速率。
在入口流率分别为1×10-3m3/s 和5×10-3m3/s条件下,开口臂长不同时,直线L1和L2上熔体的剪切速率如图6、图7所示。从6、图7可以看出,在入口流率相同条件下,开口臂长越短,直线L1和L2上熔体的剪切速率越大。入口流率不同时,直线L1和L2上熔体的剪切速率的变化曲线接近。
2.2 X 向流动速度分析
在开口臂长为15mm 条件下,入口流率不同时,直线L1和L2上熔体的X向流动速度如图8所示。从图8a可看出,直线L1上熔体的X向流动速度绝 对值在口模出口前约5mm后急剧加大,方向为X轴负向,入口流率越大,熔体的X向流动速度绝对值也越大,但是入口流率过大时,熔体的X向流动速度绝对值不增反降。从图8b可看出,在口模内起始约25mm一段距离内,熔体的X向流动速度为0,在口模出口前约5mm左右,熔体的X向流动速度方向急剧发生变化,速度方向换向,在出口处熔体的X向流动速度达到最大值。截面尺寸一致时,入口流率越大,熔体的X向流动速度绝对值越大。
在入口流率为1×10-3m3/s条件下,开口臂长不同时,直线L1和L2上熔体的X向流动速度如图9所示。从图9a可看出,开口臂长不同时,直线 L1上熔体的X向流动速度与图8中同一截面不同入口流率时熔体的X向流动速度的变化规律接近。开口臂长越短,熔体的X向流动速度绝对值越大,随着开口臂长逐渐增加,熔体的X向流动速度越来越接近,当开口臂长增加到一定程度后,熔体的X向流动速度不增反降,方向为X轴负向。从图9b可看出,开口臂长不同时,直线L2上熔体的X向流动速度在出口前约5mm方向发生急剧变化,速度方向换向,在出口处熔体的X向流动速度达到最大值,开口臂长越短,出口处熔体的X向流动速度越大
2.3 Y向流动速度分析
在开口臂长为15mm 条件下,入口流率不同时,直线L1和L2上熔体的Y向流动速度如图10所示。从图10a可知,入口流率不同时,在口模内起始约25mm的一段距离内,直线L1上熔体的Y向流动速度为0,在离口模出口处约5mm后,熔体的Y向流动速度急剧加大,入口流率越大,熔体的Y向流动速度越大。从图10b可以看出,直线L2上熔体的Y向流动速度在出口前5mm左右方向急剧变化,速度方向先正后负,熔体的Y向流动速度绝对值也在出口处达到最大值,入口流率越大,出口处熔体的Y向流动速度绝对值越大,方向为Y轴负向。
在入口流率为1×10-3m3/s 条件下,开口臂长不同时,直线L1和L2上熔体的Y向流动速度如图11所示。从图11a可看出,直线L1上熔体的 Y向流动速度在离口模出口处约5mm 位置时,熔体的Y向流动速度急剧加大,开口臂长越短,熔体的Y向流动速度越大,流动速度方向为Y轴正向。从图11b可以看出,直线L2上熔体的Y向熔体的流动速度绝对值在离口模出口处大概5mm 位置发生急剧变化,流动速度方向换向,先正向后负向,开口臂越短,熔体的Y向流动速度绝对值越大,方向为Y轴负向。
2.4 Z 向流动速度分析
在开口臂长为15mm条件下,入口流率不同时,直线L1和L2上熔体的Z向流动速度如图12所示。从图12a可看出,入口流率不同时,在口模内起始25mm的一段距离内,直线L1上熔体的Z向流动速度为0,在离口模出口处约5mm位置,熔体的Z向流动速度急剧增大,入口流率越大,出口熔体的Z向流动速度越大,方向为Z轴正向。从图12b可看出,在口模内起始25mm的一段距离内,直线L2上熔体的Z向流动速度较均匀,仅在出口前约5mm时,熔体的Z向流动速度缓慢下降。入口流率越大,出口熔体的Z向流动速度越大。
在入口流率为1×10-3m3/s 条件下,开口臂长不同时,直线L1和L2上熔体的Z向流动速度如图13所示。从图13a可知,在口模内起始约25mm 的一段距离内,直线L1上熔体的Z向流动速度为0,仅在离口模出口处约5mm时熔体的Z向流动速度急剧增大,开口臂长越短,出口熔体的Z向速度越大,方向为Z轴正向。开口臂长过长时,熔体的Z向出口流动速度也会增大。从图13b可知,直线L2上熔体的Z向流动速度在口模内起始25mm的一段距离内比较均匀,仅在出口前约5mm位置,熔体的Z向流动速度有缓慢下降趋势。入口流率相同时,开口臂长越短,熔体的Z向流动速度越大。
3 结论
通过模拟分析发现,入口流率与U型件开口臂长对刚进入口模内的一大段熔体的流动规律没有太大的影响,在该段的流速比较稳定,但在靠近出口前5mm 左右,拐角处外缘及中心线位置熔体的剪切速率及X向、Y向和Z向的流动速度都会发生很大的变化。拐角中心线附近熔体的X向、Y向流动速 度还会急剧反向。在此过程中,入口流率越大或开口臂长越短,其剪切速率及各个方向的流动速度变化越大。另外,在计算过程中假设壁面摩擦足够大,假设熔体与壁面接触处熔体的流动速度均为0,而实际实验过程中,如果能改变摩擦条件,特别是从出口前5mm 左右开始改变摩擦条件,或许会对后续的熔体流动状况大有改善。
参 考 文 献
[1] 万仕成 . PVC-U 异型材挤出成型过程中的变形问题 [J]. 化学建材,2009,25(4):8- 10.
[2] Dai Y K,Zhou C X,Yu W. Inverse designing simulation of extru-sion die of auto rubber seal and verifications[J]. Plastics Rubber and Composites,2007,36(4):141-148.
[3] Dai Yuankan,Zheng Hong,Zhou Chixing,et al . Quick profile die balancing of automotive rubber seal extrusion by CAE technology[J]. Journal of Macromolecular Science,Part A:Pure and Applied Chemistry,2008,45(12):1 028-1 036.
[4] 胡延平,魏聪,程哲,等 . 基于 UG 的塑料异型材挤出模数字化系统设计 [J]. 模具工业,2018,44(6):13-17,26.
[5] Pauli L,Behr M,Elgeti S. Towards shape optimization of profile extrusion dies with respect to homogeneous die swell[J]. Journal of Non-Newtonian Fluid Mechanics,2012,200(12):79-87.
[6] 孙乃旭,田廷科,李冰 . 基于计算机辅助的塑料异型材挤出成型工艺优化 [J]. 塑料科技,2020,48(5):103-106.
[7] 柳和生,涂志刚,熊洪槐 . 基于流率平衡的橡塑异型材挤出口模设计 [J]. 塑性工程学报,2000,7(1):76-78.
[8] 张广冬,林建平,葛友华,等 . 聚合物挤出成型模流平衡系数修正[J]. 机械工程学报,2012,48(12):75-80.
[9] 蒋标,杨卫发,张钢 . 塑料异型材挤出模模头熔体压力分析 [J].模具工业,2019,45(8):54-58.
[10] 郭凯 . 基于特征识别的塑料异型材挤出定型模 CAD 系统设计与开发 [D]. 武汉 : 武汉理工大学,2020.
[11] 柳和生,卢臣,黄兴元,等 . PTT 熔体在塑料异型材挤出口模内黏弹流动的数值模拟 [J]. 塑料,2009,38(5):98-102,4.
[12] 杨佳黎,柳和生,黄兴元,等 . Polyflow 逆向挤出功能在 T 型材口模设计中的应用 [J],塑料,2011,40(1):114-117,17.
[13] Rutgers R P G,Mackley M R. The e■ect of channel geometry and wall boundary conditions on the formation of extrusion surface instabilities for LLDPE[J]. Journal of Non-Newtonian Fluid Me-chanics,2001,98(2-3):185-199.
[14] Sienz J,Goublomme A,Luege M. Sensitivity analysis for the design of profile extrusion dies[J]. Computers and Structures,2010, 88:(9-10):610-624.
[15] 梁基照 . 聚合物拉伸流变学 [M]. 广州 : 华南理工大学出版社,2015.
[16] Ferrás L L,Afonso A M,Alves M A,et al. Annular flow of viscoelastic fluids:Analytical and numerical solutions[J]. Journal of
Non-Newtonian Fluid Mechanics,2014,212:80-91.
[17] 邓小珍 . 塑料异型材气体辅助共挤出成型的实验和理论研究[D]. 南昌 : 南昌大学,2014.











 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...














