周冬冬,陈明霞,赵金迪
(桂林理工大学机械与控制工程学院,广西桂林 541006)
摘要: 为提高橡胶挤出机Smith-模糊PID温度控制系统的控制精度,更好地实现智能整定参数与橡胶挤出机温度最优控制,采用混合粒子群(HPSO)算法优化Smith-模糊PID控制系统,完成对温度控制系统PID参数基准值的自动寻优。借助MATLAB软件辨识挤出机温控系统数学模型,搭建Smith-模糊PID温度控制系统。为避免粒子群 (PSO)算法陷入局部最优,在PSO算法的基础上将社会因子分解为局部社会因子和全局社会因子,设计出HPSO算法对PID参数进行寻优;将HPSO算法优化系统前后的控制效果进行对比。结果表明:采用HPSO算法优化Smith-模糊PID温度控制系统的控制精度更高、抗干扰性能更强,温度控制精度在±(1~1.5) ℃以内,并且接近±1℃,完全满足橡胶挤出生产过程中对料筒温度控制的指标要求,可以在一定程度上提升温控系统的控制精度以及挤出机械的智能化水平。
关键词: 橡胶挤出机;温度控制系统;模糊PID控制;Smith预估;混合粒子群算法
0 前言
橡胶具有韧性高、延展性强、绝缘性好等特点,是汽车轮胎工业必不可少的原材料。橡胶挤出机是橡胶制品挤出成型过程中的核心机械设备,对其精密控制是实现挤出半成品达到高质量标准的必要途径。挤出过程受各类波动因素的影响,其中,橡胶胶料对于温度的变化十分敏感,因此挤出机温度的波动会直接影响半成品物理性能,温度过低或过高,都会导致胶料熔融效果较差,对挤出半成品的质量造成很大的影响[1]。
在实际挤出生产过程中,对胶料品质起主要影响的是挤出机料筒部分的温控[2-3]。传统PID料筒温控系统控制精度低,无法解决料筒温控过程中存在的大滞后问题,而Smith-模糊PID料筒温控系统可以很好地解决温控过程中的滞后问题,提高温度控制精度。在料筒温控过程中,PID控制器的参数有一个基准值,而模糊PID算法就是在原PID的基础上根据误差对PID参数基准值进行动态微调。但在控制过程中,基准值是静态不变的,而且是通过人工经验调节得到的,并不是最优参数。
针对上述问题,本文作者在搭建料筒Smith-模糊PID温度控制系统的基础上,设计一种 HPSO(Hybrid Particle Swarm Optimization)算法优化Smith-模糊PID温度控制系统,实现智能整定 Smith-模糊PID控制器参数。将智能算法与Smith-模糊PID有效结合并应用于橡胶挤出机料筒温度控制中,不仅解决了料筒温控过程中存在的大滞后问题,还实现了自动寻优PID参数的基准值,提高Smith-模糊PID温度控制系统的控制精度,实现对于挤出机料筒温度的精密控制。
1、挤出机温度控制系统工艺简介
本文作者研究的主要是销钉式冷喂料橡胶挤出机,其温控系统由循环水管路和电控加热器件组成。料筒中胶料的温度主要通过电控加热器加热循环水来控制[4]。循环水通过加热器加热以后,经加压泵供给料筒的外壁流道及螺杆冷却孔中,实现胶料温度的增加。料筒循环水管路如图1所示。

图 1 料筒管路外观
当水温探测器检测到循环水温度高于设定值时,加冷却水进入循环热水中,降低循环水的温度。通过分析料筒温度控制工艺,知道文中研究的料筒温度控制系统的主要控制量是循环水的电加热器功率。具体的电控系统实物结构如图2所示。
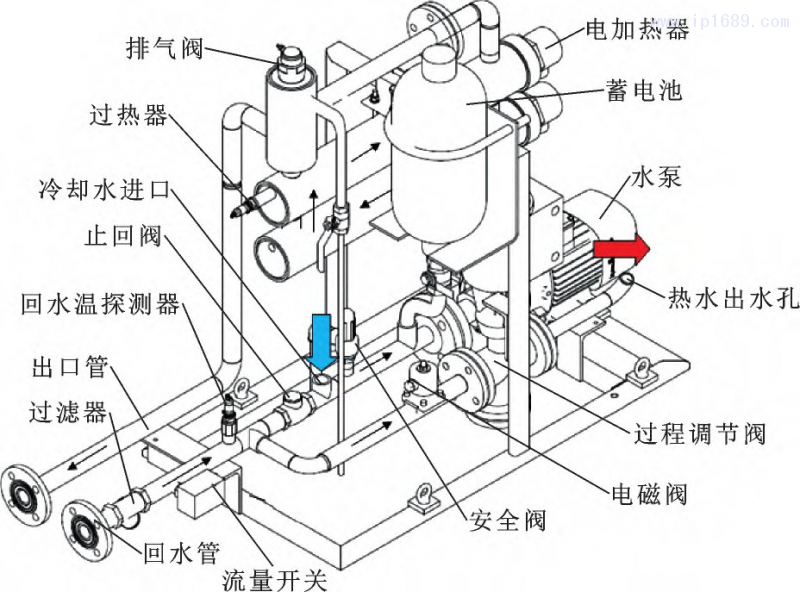
图 2 水循环电控系统实物结构
2、Smith- 模糊PID温控系统搭建
Smith-模糊PID温控系统是在模糊PID控制系统的基础上,加入Smith预估器,所以首先要搭建模糊PID控制器。根据料筒温度控制工艺结合模糊控制器选型规则,模糊控制器选取二维型。r(t) 为温度设定值,y(t)为实际检测温度值,两者的偏差e和偏差变化率ec为输入,具体结构如图3所示。
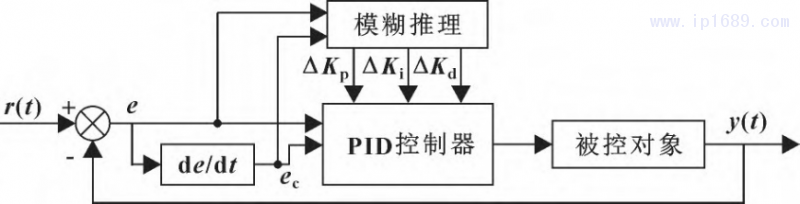
图 3 模糊 PID 控制原理
模糊控制器的模糊子集的符号以及对应的含义和数值如表1所示。

表 1 模糊规则中的符号含义
输入、输出模糊论域分别设置为 {-0.7、-0.4、-0.15、0、0.15、0.4、0.7} 、{ -0.4、-0.2、-0.1、-0.05、0、0.05、0.1、0.2、0.4} 。如图4所示,选用三角形隶属函数采用Mamdani推理法与重心法分别进行去模糊化和清晰化[5],模糊控制规则如表2所示。
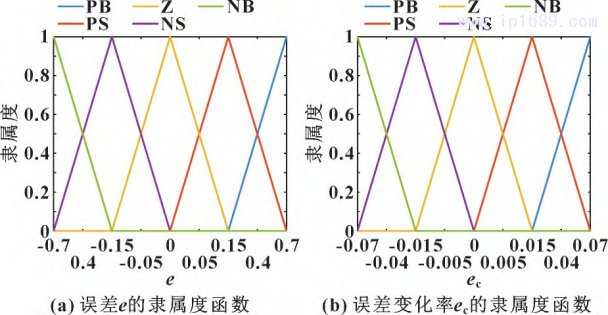
图 4 输入变量的隶属度函数
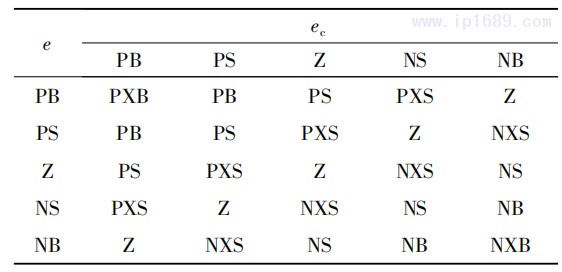
表 2 ΔKp、ΔKi、ΔKd 的模糊控制规则
在模糊PID控制器搭建完成后,继续搭建Smith预估控制器。料筒温控传递函数为
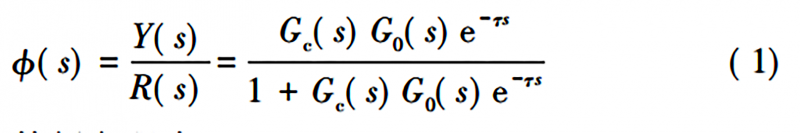
特征方程为
根据 Smith 滞后补偿原理[6],搭建Smith预估控制器如图5所示。有 Gτ(s)=G0(s) ( 1-e-τs) ,
Y*(s)=G0(s)。
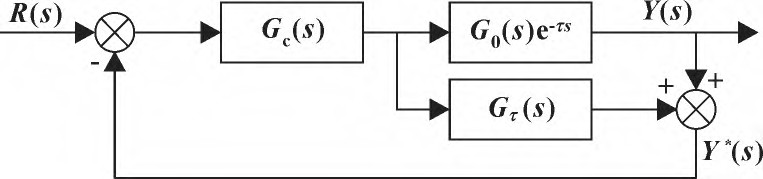
图 5 Smith 预估控制系统结构
将所搭建的Smith预估器加入到模糊PID控制器中,得到料筒温度Smith-模糊PID控制系统如图6所示[7-8]。
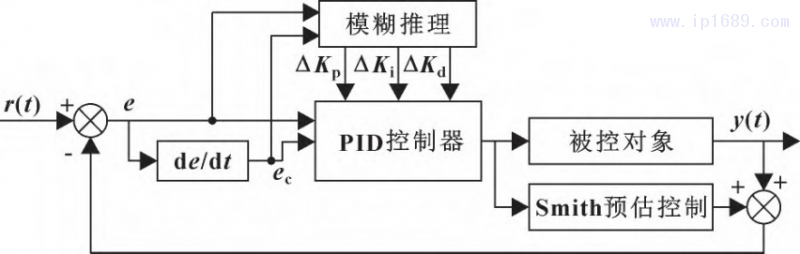
图 6 Smith-模糊 PID 控制原理
在完成Smith-模糊PID控制系统搭建后,采用HPSO算法进行优化,实现智能精准寻优PID控制参数。优化结构如图7所示。
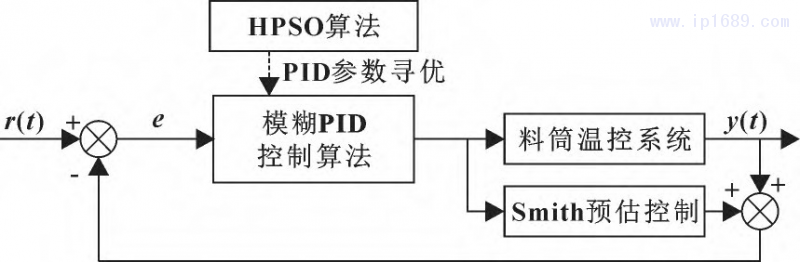
图 7 HPSO-Smith 模糊 PID 料筒温控系统结构
3 混合粒子群算法简介
3. 1 粒子群算法描述
粒子群优化 ( Particle Swarm Optimization,PSO)是一种随机搜索算法,在动态或者多目标优化环境中,更能发挥自身的优势[9]。假设群体的搜索解空间为D维,种群规模为N,第i个粒子坐标为 xi =[xi1,xi2,…,xiD]T、速度为vi=[vi1,vi2,…,viD]T,第i个粒子的历史最佳位置为Pi=[Pi1,Pi2,…,PiD]T,整个种群寻的最佳位置为Pg=[Pg1,Pg2,…,PgD]T[10]。
当搜索到以上2个最佳位置时,粒子就根据式(3) (4)更新自身的速度和位置:
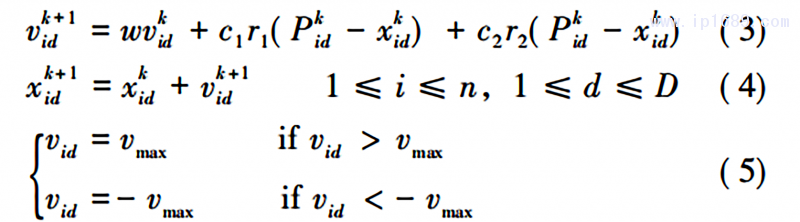
式中: w 为惯性权重; k 为当前迭代次数; vid为粒子速度,vid∈[- vmax,vmax ] ; c1和c2为粒子加速常数; r1 和 r2 为 ( 0,1) 内的随机数。
每个粒子的初速度定为0,即 v0 = 0,第j(1≤j≤ m)个粒子的下一次迭代的速度v(j)由三部分组成:
v(j) = w·v0 + c1·r·[P(j)-x(j)]+ c2·r·[PG-x(j)](6)
式中: r为( 0,1)内的随机数; v0为上一次迭代的粒子速度; w·v0 为自身惯性因子; c1·r·[P(j)-x(j)]为自身最优因子,P(j)为第j个因子自适应度最高的位置; c2·r·[PG-x(j)]为社会因子,PG为种群中自适应度最高的位置。
对于第j个粒子,第k+1次迭代的位置 x(j)k+1与第k次迭代的位置x(j)k、速度v(j+1)k关系为
式中: dt 为仿真间隔。
记前 k 次的 PG 为 P(k)G ,第k+1次迭代中适应度最高的粒子位置记为P( k+1)G ,则最终的PG为
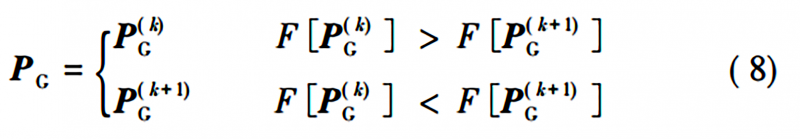
记前k次的第j个粒子的位置为P(j)k,第 k+1次的第j个粒子的位置为P(j)k+1,则最终的历史最优解P(j)为
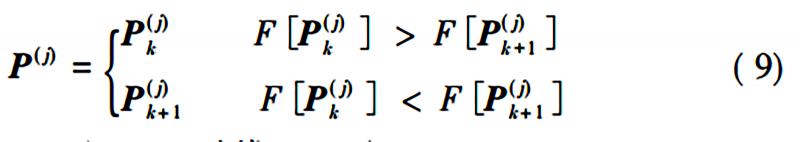
3. 2 混合粒子群算法设计
本文作者在 PSO 算法的基础上,将PSO算法中的社会因子分解为局部社会因子和全局社会因子,即得到混合粒子群( HPSO) 算法,所以HPSO算法中粒子速度可表示[11]为
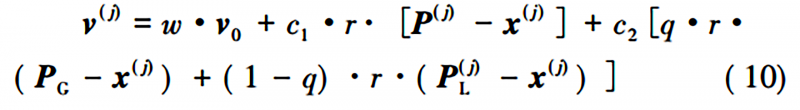
式中: 0<q<1,q为全局社会因子的占比;PG为全局最优解。P(j)与PG的计算公式在PSO算法中已给出,有所不同的是,P(j)L为第j个粒子的局部最优解坐标。
将第k次迭代的P(j)L记为P(j)L,k,第 k次迭代的第i粒子的位置为P(i)k,则有:
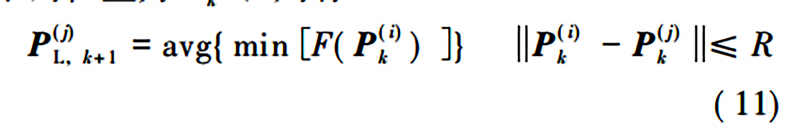
即在与第j个粒子的距离不超过R的所有粒子中,选择具有最小函数值的粒子。
3. 3 混合粒子群算法优化流程
HPSO 算法优化 Smith-模糊PID控制器参数的步骤:
步骤1,确定参数维度N、惯性系数c1、c2、w、种群规模m、迭代次数n、局部因子作用半径R;
步骤2,计算每个粒子的速度;
步骤3,计算每个粒子的自适应度 F(j)k+1 ,计算出P(j)、PG和P(j)L ;
步骤4,将上一步中的粒子依次赋值给控制器,并运行系统模型;
步骤5,输出性能指标,判断是否满足控制要求,若满足,则停止寻优; 若不满足,则继续寻优;
步骤 6,更新粒子群信息,重复上面步骤。
4 系统仿真
文中以循环水加热器的电功率P为操作变量,通过循环水温度来控制料筒温度,所以料筒温度T为被控变量。通过某五复合橡胶挤出机生产线现场所提供的实验数据,利用MATLAB辨识实验数据[12],得到料筒温度T与电加热器功率P的关系,即系统传递函数:
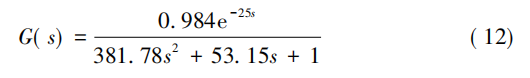
4. 1 干扰下Smith-模糊PID温控系统响应
在Simulink中搭建Smith-模糊PID料筒温度控制系统仿真模型,同时加入阶跃与非线性扰动进行仿真。料筒目标温度选取为60℃,阶跃与非线性扰动信号的幅值均设置为5,扰动作用时间为 400~480;非线性正弦扰动信号频率设置为0.05Hz,仿真结构如图 8 所示。Smith-模糊PID料筒温控系统输出响应曲线如图9所示。
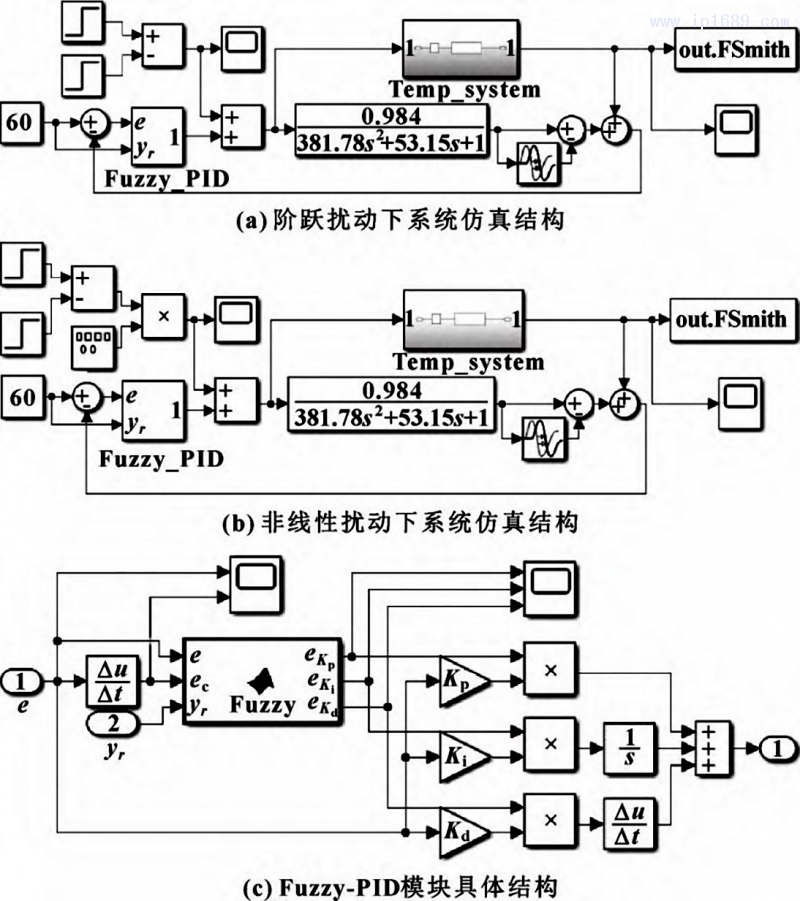
图 8 Smith-模糊 PID 料筒温控系统仿真模型
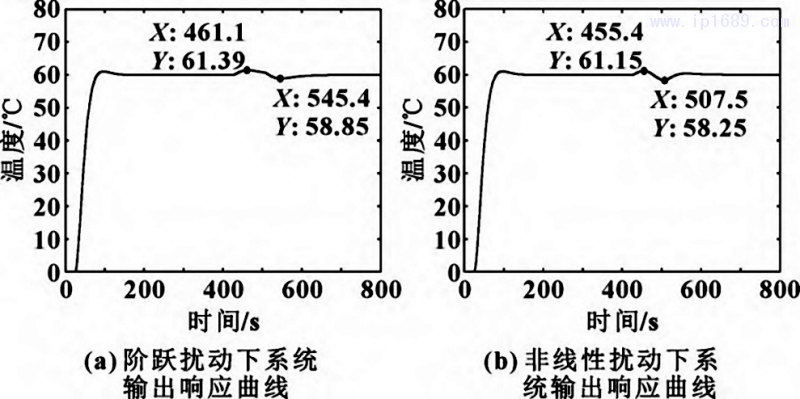
图 9 Smith-模糊 PID 料筒温控系统输出响应曲线
由图9可知:阶跃与非线性干扰作用时,Smith-模糊PID料筒温控系统响应波动幅度分别为±1.4℃和±1.8℃,在仿真进行到480s干扰作用结束时,系统基本上分别在第600s和第550s恢复到原稳定状态。结果表明:在受到干扰作用后,Smith-模糊PID控制系统能克服扰动并快速恢复到原稳定状态,并且温度控制精度在±2℃以内。由于橡胶挤出工艺中料筒温度控制性能指标要求为±( 1~1. 5)℃,所以料筒温度 Smith-模糊PID控制系统还没有完全达到控制精度要求,因此采用HPSO算法进一步优化。
4. 2 HPSO优化Smith-模糊PID温控系统
HPSO算法参数设定:种群规模为50,最大迭代次数为20,位移仿真间隔dt为0.3,w为2,c1为2,c2为2,xmax为10、0. 1、10,vmax=0. 5xmax,局部社会因子ρ为0.4,局部因子作用半径R为0.2。进行5次仿真实验,得到 HPSO算法优化 Smith-模糊PID控制器的响应曲线,如图10所示。HPSO算法优化信息如图11所示。PID参数随迭代次数变化如图12所示。
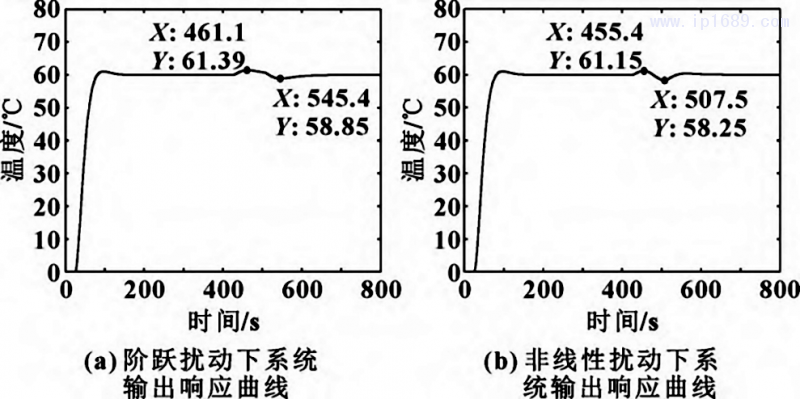
图 10 HPSO 优化 Smith-模糊 PID
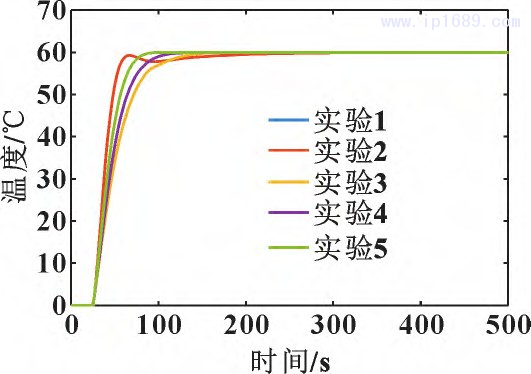
图 11 HPSO 优化 Smith-模糊 PID 系统信息曲线
图 12 PID 参数随迭代次数的变化
由图10可以看出:随着迭代的进行,系统输出响应越来越好。由图11可以看出:迭代优化到第7次以后,调节时间稳定,而且调节时间曲线波动较少,系统无超调量且保持稳定,评价函数随优化过程波动小并逐渐稳定。由图12可以看出:随着迭代优化7次后,3个参数的相对值稳定不变,最终得到HPSO优化Smith-模糊PID控制器的3个参数Kp、Ki、Kd分别为2. 657 8、0. 054 2和8. 360 4。
4. 3 HPSO 优化前后抗干扰性对比
为验证HPSO算法优化的 Smith-模糊PID系统具有更好的抗扰性能,在相同扰动情况下对比分析 HP-SO 算法优化的 Smith-模糊PID控制系统与Smith-模糊PID控制系统的抗扰性能。扰动数值设置与前面相同,得到阶跃扰动下、非线性扰动下系统抗扰性输出曲线分别如图13和图14所示。
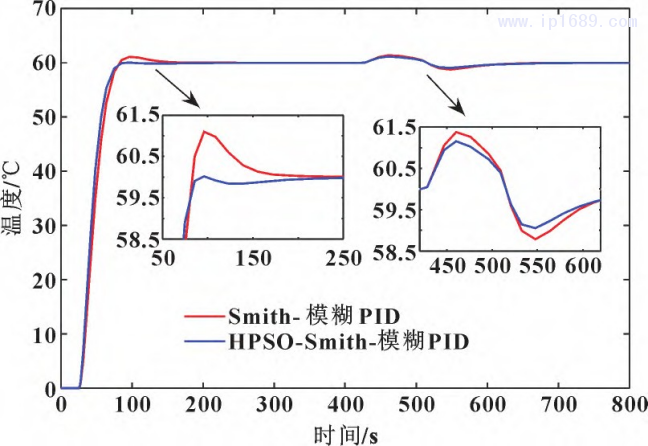
图 13 阶跃扰动下HPSO 优化 Smith- 模糊PID前后抗扰对比曲线
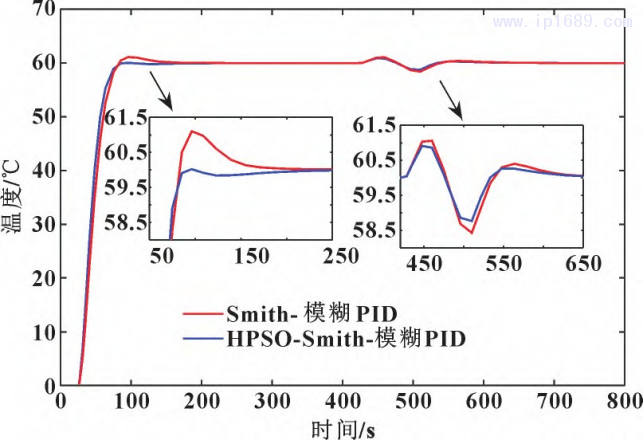
图 14 非线性扰动下 HPSO 优化 Smith- 模糊PID前后抗扰对比曲线
由图13、图14可以看出:HPSO算法优化后的系统动态响应无超调,而优化前的系统有大约2%的动态超调;在阶跃干扰作用下,优化后系统受干扰的波动幅度为±1.1℃,优化前系统受干扰的波动幅度为±1.4℃; 在非线性干扰作用下,优化后系统受干扰的波动幅度为±1.2 ℃,优化前系统受干扰的波动幅度为±1.6℃。结果表明:HPSO-Smith模糊PID控制系统的动态响应无超调、稳态误差为零,温度控制精度在± (1~1.5)℃以内,并且接近±1℃ ,能够快速地跟踪并抑制料筒温度的变化。
5 结束语
基于Smith-模糊PID控制器,在PSO算法的基础上设计出HPSO算法优化Smith-模糊PID控制系统,用于橡胶挤出机料筒温度控制。HPSO算法优化后的Smith-模糊PID控制系统在动态响应与抗干扰性能方面都比Smith- 模糊PID 控制系统有所提升。采用HPSO算法完成对PID参数基准值的自动寻优,从而使系统输出响应具有较好的动态与稳态性能。结果表明:在线性与非线性干扰作用下,HPSO算法优化的Smith-模糊PID温度控制系统仍具有良好的鲁棒性与自适应性,温度控制精度在±(1~1.5)℃,并且接近±1℃,完全满足橡胶挤出生产过程中对料筒温度控制的指标要求,能够较好地实现橡胶挤出机料筒温度的精准控制。
参考文献:
[1] 王文昌. 影响精密挤出稳定性的因素分析[J]. 化工管理,2015( 10) : 186-187.
[2] 孙若武.橡胶挤出机温度压力控制系统的研究[D]. 沈阳: 东北大学,2014.
[3] 张临松,王士军,陈伟,等. 塑料挤出机的多路温度控制系统设计[J].自动化与仪表,2018,33(11) : 29-32.
[4] 李晓林.单螺杆精密挤出机理的研究[D]. 北京: 北京化工大学,2003.
[5]边志坚.模糊 PID 在铸锭炉温控系统中的应用研究[D].石家庄: 河北科技大学,2015.
[6] 李全俊,黄权,李锦. Smith 预估模糊自适应 PID 控制在时滞系统中的应用[J]. 兵工自动化,2011,30(12) : 49-52.
[7] 高锦,章家岩,冯旭刚,等.基于失配补偿 Smith-RBF神经网络的主蒸汽压力控制技术[J]. 重庆大学学报,2019,42( 7) : 105-113.
[8] 刘晴,李鸿.基于 Smith 预估模型+模糊 PID 的地铁列车空调控制[J].工业控制计算机,2019,32(11) : 95-96.
[9] 王大志.面向实际工程问题的粒子群优化算法应用技术的研究[D].沈阳: 东北大学,2009.
[10] 史峰,王辉,郁磊. MATLAB 智能算法 30 个案例分析[M].北京: 北京航空航天大学出版社,2011.
[11] 张庆科.粒子群优化算法及差分进行算法研究[D]. 济南: 山东大学,2017.
[12] 杨丽娟.热电堆传热过程的数学建模与实践[D].杭州:杭州电子科技大学,2015.
[13] 盛凯.冷喂料挤出机的温度控制系统[J]. 橡塑技术与装备,2001,27(11) : 52-54.
[14] 赵金龙.销钉式冷喂料挤出机供胶系统在轮胎钢丝帘布压延中的应用[J].橡胶科技,2016,14(6) : 39-42.
[15] 陈超,陈乐庚,谭开顺,等.橡胶冷喂料挤出机综合控制方法[J].橡胶工业,2012,59(10) : 626-630.












 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...














