赵南阳1,许忠斌1,**,林增荣2,叶如清2,成明祥2
(1.浙江大学化工机械研究所,浙江 杭州 310027; 2.德清申达机器制造有限公司,浙江 湖州 313200)
摘要:双曲肘五孔斜排合模机构因其优异的运动特性和增力效果在注塑成型领域有着广泛应用。为解决注塑机合模机构设计过程参数众多、计算复杂、设计低效、寻优困难等问题,基于开合模过程的运动与受力特性细节,对双曲肘五孔斜排合模机构进行数学建模,引入有约束非线性优化计算,开发了一套集结构分析计算和多目标优化的合模机构设计系统FJTC。该设计系统可适用于不同注塑机应用场景,可针对行程比(Ks)、增力倍数(M)、行程比/增力倍数等不同的需求开展优化设计,大幅提高设计效率;另可集成在Web端,方便技术人员开展设计,满足了企业生产实际需求。
关键词:多功能; 集成系统; 合模机构; 优化设计; 注塑机; Matlab
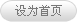
注塑机合模机构按工作原理可分为机械式、液压式和液压机械组合式三种形式[1]。其中机械式合模机构利用各种形式的肘杆机构,按结构可分为内翻/外翻式五孔斜排双曲肘合模机构、内卷式四孔斜排肘杆合模机构、五孔直排式合模机构等,其中,双曲肘五孔斜排合模机构(如图1所示)具有增力效果好、运动特性优异、机构紧凑、油路简单、工作可靠、成本较低等优点[1-6],在锁模力5~3600t的各类型微注塑机和大型注塑机上均取得了广泛应用。

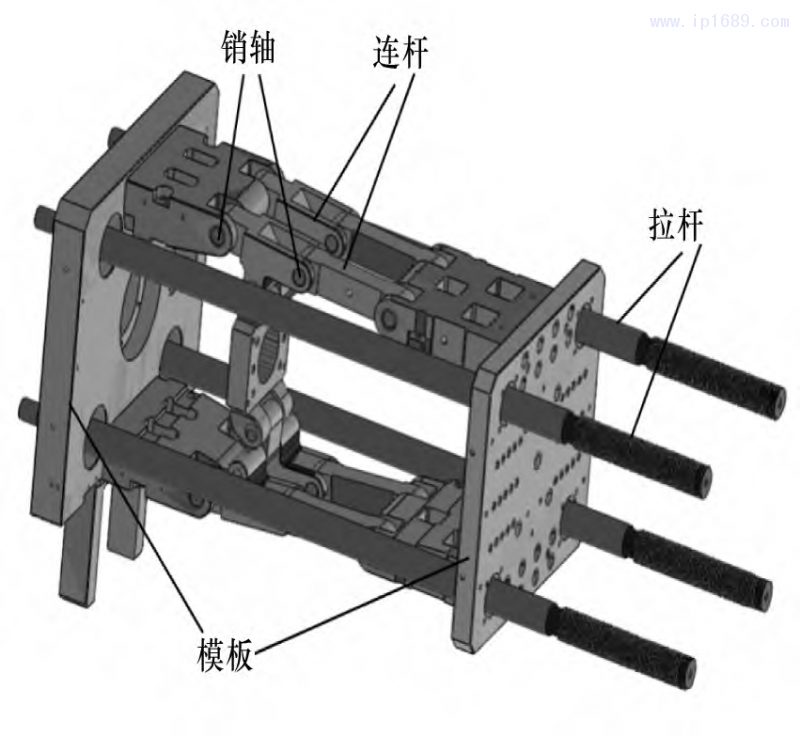
a-合模机构组件 b-合模机构组成
图 1 典型的双曲肘五孔斜排合模机构
双曲肘五孔斜排合模系统的机构参数较多,不易直观分析,计算过程也非常复杂[7-14]。开发出一套可方便计算合模机构的结构尺寸、提高设计人员效率和注塑机设计水平的新型多功能集成设计系统是目前国内外注塑行业发展的迫切需要。华南理工大学在大量工程经验和理论分析的基础上建立了一套体系完整、简洁可靠的肘杆式合模机构工程设计的数学模型[15-16]。但随着注塑机品种的多样化和不同工程应用的发展,该模型需要根据工程实际进行改进。北京化工大学经过多年的研究建立了自己的肘杆式合模机构设计体系并开发了配套的设计软件[6,12,17],然而,该设计方法在推导过程中表达复杂程度高。台湾科技大学射出成形实验室推出的合模机构设计过程优化系统[18]在富强鑫注塑机上得到了验证,该系统部分设定参数的表达和检验上与中国大陆有区别,无法在中国大陆进行推广。针对复杂的工程应用面向多样化的注塑机结构,开发集成化程度高、推导过程简洁、以国内环境为依托的新一代设计系统符合当下的时代需求,可为合模机构的设计与优化提供理论窗口和技术支持,具有深远的应用前景。
本课题组在上述研究的基础上,将有约束非线性优化引入计算模型,结合速度瞬心法和虚位移原理改进修正合模机构运动学和受力分析理论,开发了一套集结构分析计算和多目标优化的集成设计系统,大大降低了计算的复杂度,提高了设计精度。该系统可针对行程比(Ks)、增力倍数(M)、行程比/增力倍数等不同的功能需求开展优化设计,可分析肘杆尺寸和夹角对与增力倍数、动模板与十字头速度比及动模板加速度等多参数之间的变化关系,实现了合模机构多功能集成设计。
1合模机构运动与受力特性
为了对注塑机双曲肘五孔斜排合模机构的参数进行计算,合模机构各杆长、夹角等参数定义如图2所示。考虑到双曲肘五孔斜排合模机构上下对称的结构,取模板中心线一侧进行分析研究[11,19-21],图2显示了双曲肘五孔斜排注塑机合模机构开合模的运动简图。
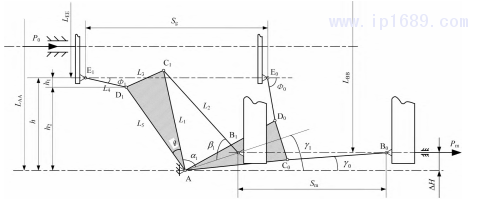
图 2 双曲肘五孔斜排合模机构开合模运动简图
LAA-后模板对称铰A的中心距离;LEE-十字头中心距;LBB-动模板中心距;Sg-油缸行程;Sm-合模行程; M-增力倍数; ΔH-铰A和铰B之间的垂直 距离; h-固定铰A与十字头铰座E的垂直距离; h1-铰座D与十字头铰座E的垂直距离;h2-固定铰A与铰座D的垂直距离; L1-后连杆AC长度; L2-前连杆CB长度; L3-中间杆AD的长度; L5-中间杆CD的长度; L4-推力杆DE长度; λ-肘长AC和CB的比值; θ-连杆AC和CD的夹角; Φ-连杆DE与水平线的夹角; α-连杆AC和铰A和B的连线之间的夹角;β-连杆AB和CB之间的夹角; γ-铰A和B的连线与水平线之间的夹角; C-系统刚度; 脚标“1”-开模位置的尺寸角度信息; 脚标“0”-最终合模位置的尺寸角度信息。
1. 1 运动分析
铰座C的移动量可用于表征动模板的合模行程(Sm) ,铰座E的移动量可用于表征油缸行程 (Sg)。动模板的Sm和Sg的数学表达式[15,22-25]:
Sm=LAB0cosγ0 -LAB1cosγ1 (1)
Sg=L5[cos (γ0+θ)-cos (γ1+α1+θ)]+L4(cos Φ1-cosΦ0) (2)
式中,LAB0-合模时AB间的距离; LAB1-开模时AB间的距离。
LAB0=L1+L2 (3)
LAB1=ΔH/sinγ1 (4)
合模机构行程比( Ks )为:
Ks = Sm/Sg
根据速度瞬心法[15,18,26],可以确定计算合模速度(Vm)和速度变化系数(Kv) :
式中,VB和VE分别表示铰座B和铰座E的速度。不计合模机构运动过程中各杆件的变形,动模板加速度(ɑm) 可表示为:
式中,w1-AC 杆的角速度; w2-CB 杆的角速度; w4-ED 杆的角速度; ε1-AC 杆的角加速度。
1.2 受力分析
根据虚位移原理[15-16],可以获得合模机构的增力倍数(M):
式中,P0-油缸推力; Pm -合模力。可见增力倍数M随着α变化,为了便于比较,根据经验,此处取α=2°时的M作为增力倍数的参考值。
根据连杆机构的增力倍数表达式可以得到增力倍数(M)和速度变化系数(KV)成倒数关系,表明了连杆机构的增力和增速是相互矛盾的,因此,需要合理确定增力倍数以确保机器性能的综合性能[15]。
2 合模机构的优化设计
2.1 目标函数
在双曲肘五孔斜排注塑机合模机构的设计过程中,通常会按如下要求对机构进行优化:1)追求最大行程比,即max{Ks},其设计思想是在合模机构活塞行程相同的条件下,使其动模板行程最大,即动模板平均速度最大。此目标函数有利于提高注射成型机的启闭模效率,提高空循环次数,缩短成型周期;2)追求最大增力倍数,即max{M},追求增力倍数有利于提高合模力,降低能耗,并且有助于提高产品质量; 3)追求多目标优化,即max{Ks,M},其设计思想是选择合适的技术指标参数,以确保机构性能整体最优。目标函数的表达式如式(14)所示:
F ( x) = - ( x1 n1 K +x2 n2 M) ( 14)
式中,x1和x2分别代表合模机构的行程比( K s ) 和增力倍数( M)的权重系数,需根据实际情况调整,本文中x1 = 1,x2 = 1/18; n1和n2表示优化目标定位系数,为布尔量。
2.2 设计变量
设计变量是优化设计过程中重要的参数,需要综合考虑: 1)难度和计算量;2)机构的综合性能两个指标[17]。双曲肘五孔斜排注塑机合模机构结构复杂,参数较多,并且要排除相互干涉的参数。经综合分析,最终确定 L1、L2、L4、L5、h、γ0、θ七个参数为设计变量。
X=[L1,L2,L4,L5,h,γ0,θ]
=[X1,X2,X3,X4,X5,X6,X7] ( 15)
2. 3 约束与边界条件
双曲肘五孔斜排注塑机合模机构的约束条件包括性能约束条件和几何约束条件。为了避免双曲肘合模机构各部件的自锁和干涉现象,需要对合模机构后连杆L1与前肘杆L2的长度比λ、行程比Ks、增力倍数M、临界锁模角αL、初始角α1和φ1、后连杆长度L1、A铰座与B铰座之间的距离 (LAB1)进行约束:

式中,Δ1-连杆L1两肘相对间隙; Δ2-销孔A和B孔壁间实体最小间距; DC-铰C销轴衬套外径; DA-铰A销轴衬套外径。
在不同影响收敛的前提下,设计变量的边界条件需根据具体的结构设计参数进行确定,本文的实例中边界条件为:
3 实例分析
3.1 结构化设计与优化设计
以1300 kN大行程比双曲肘五孔斜排注塑机的合模机构为例对该多功能集成系统开展验证。依次进行:拉杆设计、连杆设计、销轴及衬套设计、模板设计、杆件长度及相关角度设计、约束条件检查及验算等。
初始化参数如表1所示,合模机构拉杆模板等结构件的材料选择见表2所示,开展结构化设计,获得可行的杆件结构参数; 随后开展优化设计,得到的结构化设计结果与优化设计结果,如表3所示,其中优化圆整主要对后连杆AC、前连杆AB以及中间杆AD的水平与垂直距离进行近似。
表1 初始化参数

表2 结构件材料

表 3 结构化设计和优化设计结果
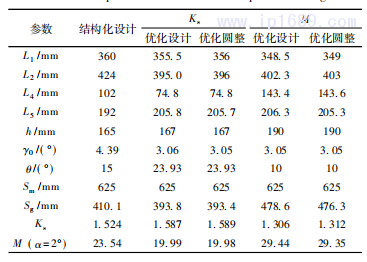
由表3可得,本集成系统设计可对双曲肘五孔斜排注塑机合模机构拉杆、连杆长度以及各杆件间的夹角进行精确计算。本案例中,保证合模行程Sm为625mm不变,对原有的结构参数开展优化。以行程比Ks为优化目标 (n1=1,n2=0),在保证增力倍数合理的同时,行程比由1.524上升至1.589,行程比得到提高。L1和L2的总和由784mm降至752mm,降低了4%,可以在保证机构有效功能的同时,降低机器的长度,减少占地面积。以增力倍数M为优化目标( n1=0,n2=1) ,合模机构L1和L2的总和由784mm降至752mm,降低制造成本,提高空间利用率。增力倍数M由23. 54增至29. 53,增长了25. 4%,降低了能耗,优化效果显著。
3. 2 速度比分析
图3表示合模过程中原设计方案与优化方案中动模板与十字头之间的速度比Kv随着合模行程的变化曲线。由图可知,动模板运动过程经历了“慢-快-慢-快”的过程,合模前的增速使合模机构形成预应力,确保前后模具间的锁紧配合。按行程比Ks优化的结果与原设计方案相比,在合模行程小于100mm时速度比差别较小,最大速度比由2.55增至2.56,优化后整个过程的合模平均速度有所提高,模具的开合模过程启动更加迅速,且模具速度波动与原设计相比变化较小,按行程比 Kv优化后的合模机构有助于提高生产效率。按增力倍数M优化后的合模机构速度比 Kv 降低,合模行程小于100mm与合模行程大于450mm时,速度比显著低于原设计方案,最大速度比降低至2.36,平均速度降低,速度波动程度基本不变,合模机构运动过程更加平稳,有效缓解前后模之间的冲击作用。
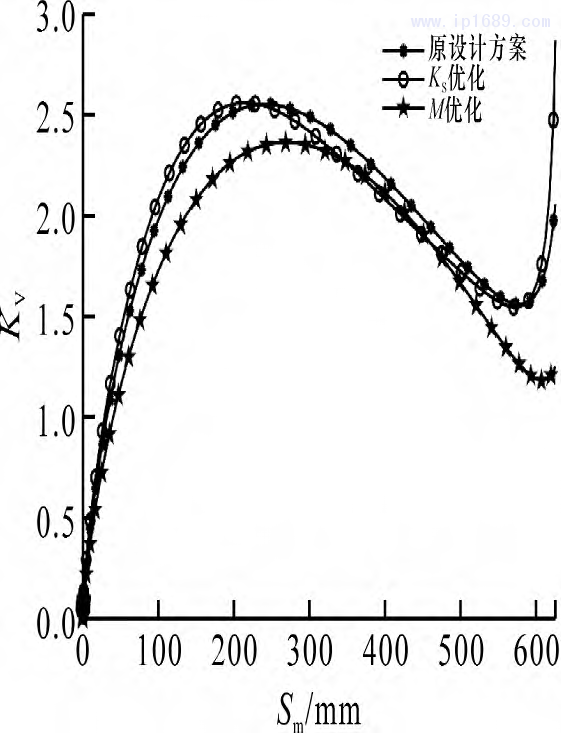
图3 速度比 K v 曲线
图4显示了各优化方案与原设计方案的动模板加速度变化规律。按行程比Kv优化后的动模板加速度am曲线在合模启动时最为陡峭,加速效果最明显,在合模行程为180mm附近出现零点,随后合模机构开始减速。以增力倍数M为优化目标的动模板加速度am曲线最为平滑,机构在合模启动和终了时加速度为0,合模过程中加速度在合模行程为250mm时出现零点,出现零点的过程也最迟缓,合模运动过程中启停最平稳,冲击更小。
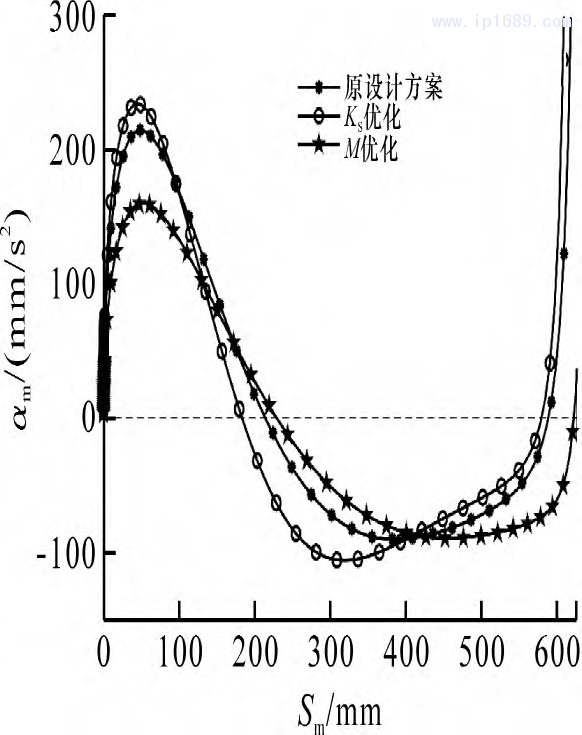
图4 动模板加速度am曲线
3. 4 增力倍数分析
图5显示了优化方案由原设计方案的增力倍数M曲线。以行程比 Ks为优化目标的合模机构的增力倍数M(α=2°) 有所降低,从23.54降至19.98,降低了15%,提高行程比的同时,保证了增力倍数有效取值。以增力倍数M为优化目标的合模机构增力倍数M(α=2°) 上升至29.44,提升27%,降低能源的消耗,优化效果显著。
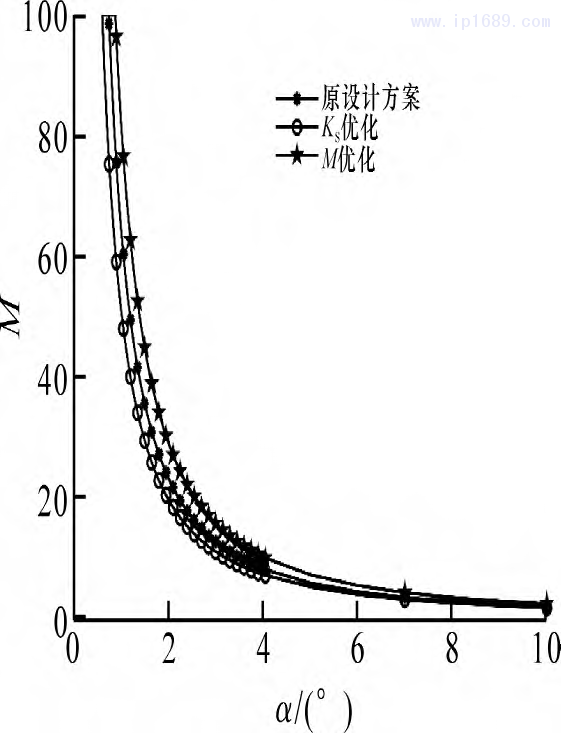
图5 增力倍数M曲线
3. 5 合模机构设计系统Web平台部署
利用Matlab配套的MatlabWebAppServer对本多功能集成设计系统进行Web端部署,使用者可以在不安装Matlab的情况下,在Web端进行设计计算,极大地便利了设计人员,系统在Web端运行界面如图6所示。

图 6 多功能集成设计系统主页
4 结论
本文详细分析了双曲肘五孔斜排注塑机合模机构的运动与受力特性,结合合模过程的运动学和动力学特性细节,对合模机构工作过程进行建模分析,推导改进了合模机构的行程比Ks、速度比Kv、动模板的加速度am、增力倍数M的计算过程,降低了计算的复杂度,为注塑机双曲肘五孔斜排注塑机合模机构的多功能集成设计系统 (FJTC系统) 的开发提供了理论基础。
开发的双曲肘五孔斜排注塑机合模机构的多功能集成设计系统 (FJTC系统) 实现了合模机构的结构设计、优化设计及Web端应用的集成整合。该系统的应用将有效改进注塑机合模机构的运动特性,降低合模保压过程能耗,提高合模机构运动的精度和平稳性,也有利于提高注塑制品的质量和延长注塑设备的使用寿命。经相关企业的应用实践检验,它在增力倍数的改善与设备尺寸的降低上也有显著的效果,对新型高性能注塑机的开发具有重要的应用价值。
参考文献
[1] 王兴天.注塑工艺与设备[M].北京: 化学工业出版社,2009:460-592.
[2] LEI C J,YU J H,ZHAN H F,et al. Multi-objective op- timization design for double toggle clamping unit of injection molding machine[J]. Applied Mechanics and Materials,2012,1968 (201-202):15-19.
[3] HUANG M S,NIAN S C,CHEN J Y,et al. Influence of clamping force on tie-bar elongation,mold separation,and part dimensions in injection molding[J].Precision Engi-neering,2018,51: 647-658.
[4] ZHAO N Y,LIAN J Y,WANG P F,et al. Recent pro- gress in minimizing the warpage and shrinkage deformations by the optimization of process parameters in plastic injection molding: A review [J].The International Journal of Advanced Manufacturing Technology,2022,120: 85-101.
[5] 王喜顺,屈长龙. 注塑机曲肘式合模机构弹性动力分析与优化[J].塑料工业,2015,43 ( 3) : 68-75.
[6] 赵世超,鉴冉冉,谢鹏程,等. 注塑机合模技术探讨与发展[J].塑料,2018,47 ( 2) : 75-78.
[7] LIN W Y,HSIAO K M . Study on improvements of the five-point double-toggle mould clamping mechanism [J]. Proceedings of the Institution of Mechanical Engineers,Part C: Journal of Mechanical Engineering Science,2004,218 (7) : 761-774.
[8]PARK S,BAE J,JEON Y,et al.Optimal design of toggle-linkage mechanism for clamping applications [J]. Mechanism Machine Theory,2018,120: 203-212.
[9] 康玉辉,千红涛. 基于 ADAMS 的注射机双曲肘合模机构研究[J]. 塑料科技,2019,47 ( 12) : 108-111. KANG Y H,QIAN H T. Research on double-toggle clam- ping mechanism of injection molding machine based on AD-AMS [J].Plastics Science and Technology, 2019, 47 ( 12) : 108-111.
[10] 申军伟. 基于MATLAB软件GUI技术的双曲肘合模机构优化程序设计[J].机械研究与应用,2019,32 ( 4) : 173-174.
[11] 申军伟,程珩. 基于关联特性的注塑机合模机构运动特性研究 [J].中国塑料,2013,27 (4) : 90-94.
[12] 王诗强,谢鹏程,何雪涛,等. 基于MATLAB 的注塑机合模机构优化设计及系统开发[J].工程塑料应用, 2013,41 ( 5) : 54-57.
[13] 郭永增. 基于多软件协同的电动合模机构的优化[J].橡塑技术与装备,2020,46 ( 22) : 46-49.
[14] 于盛睿,凌妍,邹佳勇,等.全电动注射机位置系统的回零算法设计与实现[J].工程塑料应用,2020,48 ( 11) : 85-90.
[15] 冯良为. 五孔斜排双曲肘合模机构的运动和力分析[J]. 塑料科技,1996 (4) : 35-38.
[16] 冯良为,岑运福.注射成型机五孔直排式合模机构的运动和力学特性分析[J].种橡胶制品,2002,23 (2) : 40-42.
[17] 熊万春.曲肘式合模机构的结构参数优化[D].北京:北京化工大学,2008.
[18] HUANG M S,LIN T Y,FUNG R F.Key design param- eters and optimal design of a five-point double-toggle clam- ping mechanism[J]. Applied Mathematical Modelling, 2011,35(9) : 4304-4320.
[19]付琳,欧宇,唐承辉,等. 全电动注塑机设备合模机构结构优化[J].塑料科技,2021,49 (7) : 121-123.
[20] 张友根. 注塑机肘杆合模机构弹性变形关联特性的研究[J]. 塑料制造,2011 ( 5) : 72-79.
[21] 钟士培. 注塑机双曲肘合模机构运动仿真研究[J]. 装备制造技术,2010 ( 3) : 6-7.
[22] LI X W,JIN Z M ,ZHANG Y J,et al. Kinematic cal- culation analysis of micro injection molding machine with double-toggle clamping mechanism based on MATLAB[C] / /2nd International Conference on Electronic and Me-chanical Engineering and Information Technology ( EMEIT ) , Netherlands: Atlantis Press, 2012: 1746-1750
[23] 董凌波,张哲衍,李国平,等. 基于最小速比偏差的注塑机双曲肘合模机构优化设计[J].宁波大学学报 ( 理工版) ,2021,34 (1) : 39-44.
[24] 刘晓彬,杨于光,董力群,等. 基于遗传算法的全电动注塑机双曲肘内翻式合模机构优化设计[J].塑料, 2016,45 (5) : 17-21.
[25] 王国宝,程珩,李福,等. 注塑机双曲肘合模机构的优化设计研究[J].工程塑料应用,2011,39 (5) : 87-90.
[26] BALASUBRAMANYAM C, SPANDANA K R, AJAY M S,et al. Optimization approach for synthesis of 5 point double toggle mechanism [J].International Journal on In- teractive Design and Manufacturing ( IJIDeM ) ,2017,11 ( 4) : 839-850.












 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...














