周乐东,唐胜峰,黄铁平,高国利
(深圳银宝山新科技股份有限公司技术中心,广东 深圳 518108)
摘要:根据多项式回归理论,用数学语言描述注塑机的电机传动系统过渡惯性对V/P切换位置控制的影响,并构建了二者的拟合曲线函数,能够预测任意速度下V/P切换位置的控制误差,预测结果可以对注塑机设定值进行补偿,提高注塑机V/P切换位置控制的稳定性。
关键词:注射工艺优化;过渡惯性;V/P切换;工艺波动;控制精度
0 引言
注塑机是国内产量和应用量较大的塑料成型设备,注射生产是整个塑料产业中最能体现核心技术价值的领域[1]。随着用户对塑料制品品质要求的不断提高,注射成型逐渐向精量化方向发展,针对提高注塑机工艺控制稳定性的研究越来越多。刘立柱[2]以1600kN的双色注塑机为研究对象,通过研究其液压系统并建立相应的数学模型,提高了液压控制系统的稳定性和油液使用效率;康存峰等[3]根据连杆机构的运动学原理,利用Matlab拟合位移和速度的关系曲线,保证了注射成型过程中锁模力的稳定性。
电机驱动和PLC控制技术提高了注塑机的控制精度,但是由于电机传动系统过渡过程中存在惯性,如机械惯性、电磁惯性等,使设备设定的目标参数与实际运行的结果之间出现偏差,典型的如V/P切换位置的波动,注塑机V/P切换是电机传动的过渡过程,会受到过渡惯性的影响,因而导致在不同的注射速度条件下,V/P切换控制的执行结果各不相同。董召然[4]在对比了几种常规注射保压切换方法后,指出其不足之处,提出更加合理而有效的二维模糊推理的注射保压切换方法。另一方面,注射仿真分析工具的普及促使工程人员开展了许多基于模流分析的注射工艺优化方法研究,如唐杰等[5]结合汽车灯罩的实际注射情况进行CAE仿真分析研究,优化了工艺参数;王策等[6]针对电池盖板的注射工艺仿真分析,将其变形量降低了23%。这些研究改变了过去试模普遍采用通过观察上一模注射试验的结果来决定下一模工艺设置策略的“试凑法”,倡导根据模流分析确定目标参数指导注射工艺优化的新模式。然而在实践过程中,注塑机自身结构特性带来的影响导致目标和实际存在一些偏差,这些偏差会阻碍目标参数的现场应用,使模流分析的成果并未真正有效地促进注射生产企业效益提升和技术进步。
为研究注塑机V/P切换控制产生偏差的机理,现以1200kN的电动注塑机为研究对象,针对注塑机电机传动系统过渡惯性的影响,开展不同注射速度的V/P切换位置波动规律的研究,并通过构建注射速度和V/P切换位置波动量之间的函数关系式,表达电动注塑机传动系统过渡惯性对V/P切换位置控制造成的影响。
1 V/P切换控制的执行过程
V/P切换是指注射过程中,模具型腔即将被熔体充满时,注塑机的螺杆运动由速度控制转变为压力控制,以便熔体更加平稳地充满型腔。V/P切换的控制有压力控制、速度控制、时间控制以及位置控制等多种方式,其中位置控制的稳定性和可靠性最好,应用最广泛。
V/P切换位置控制的实现需由操作者预先设定一个螺杆位置参数,在注射阶段,当注料系统内的螺杆位置传感器侦测到螺杆运动到设定的位置时,反馈信号给注塑机控制系统,控制系统执行V/P切换指令,使螺杆的运动方式由恒速驱动转变为恒压驱动。在此过程中,由于存在螺杆运动的机械惯性、传动电机的电磁惯性、信号反馈延时等因素,实际完成V/P切换时对应的螺杆位置会大于操作者设定的值。注塑机的这种特性使操作者在确定合适的V/P切换位置时总会面临需要反复调试的问题,如试模过程中常出现相同V/P切换设定参数注射的样件填充状态却不相同,即在某种注射速度条件下合适的V/P切换位置在另一种速度下并不适用。
2 V/P切换位置波动研究试验
2.1试验方法
为研究材料黏度和注射速度对注塑机V/P切换位置控制稳定性的影响,设置材料种类、注射速度和熔体温度3组变量进行试验,采集各组试验设定V/P切换位置和注射终点数据,以设定V/P切换位置和注射终点的差异描述注塑机V/P切换位置控制的稳定性,差异越小,稳定性越好。
利用试验模具(见图1)在1200kN电动注塑机上分别用5种不同的材料(见表1)进行试验,注塑机的最大注射速度为200mm/s,试验的注射速度限定在10~180mm/s,同时试验旨在研究V/P切换位置的波动,无需进行保压过程,试验的保压时间均设置为0。
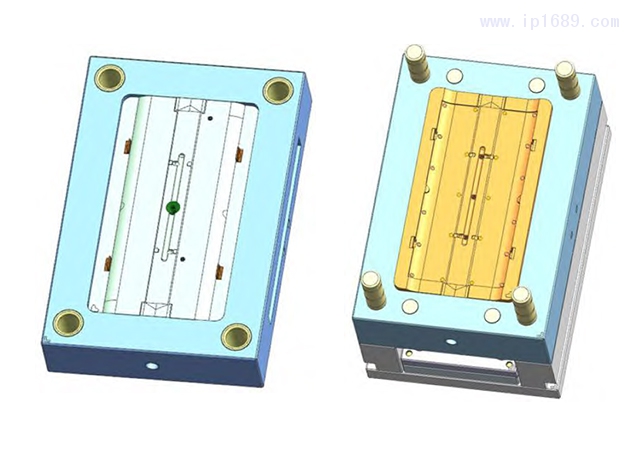
图1 试验模具
2.2 试验数据收集
每组试验条件下注射5模次,采集第5模的V/P切换设定位置S和当前模次的螺杆位置曲线最小值S',S'即为实际的注射终点,再计算设定位置和实际注射终点的差值△S=S-S',定义△S为当前注射速度下V/P切换位置的波动量,△S反应了注塑机注射传动系统的过渡惯性对V/P切换位置控制的影响。
3 试验数据分析
3.1 试验数据整理
试验数据显示各种材料在同一注射速度条件下,V/P切换位置波动△S均相同,熔体温度对△S没有影响,表明△S与材料黏度无关。试验数据还显示△S随注射速度的升高而增大的规律,如图2所示。统计学中常用皮尔逊(Pearson)积矩相关系数度量2个变量之间的相互关系,皮尔逊积矩相关系数定义为2个变量的协方差与二者标准差积的商,一般用R表示。假设样本标记为(Xi,Yi),则其Pear-
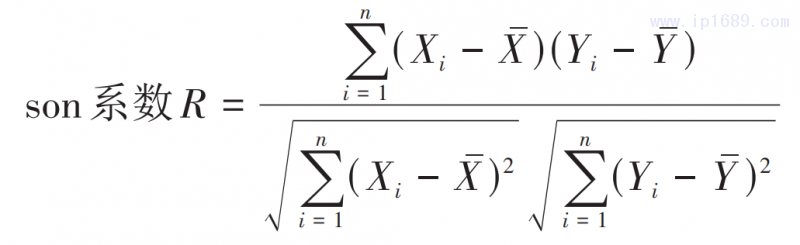
通过计算△S与V数组的皮尔逊(Pearson)系数为0.975,反应二者存在强关联关系。
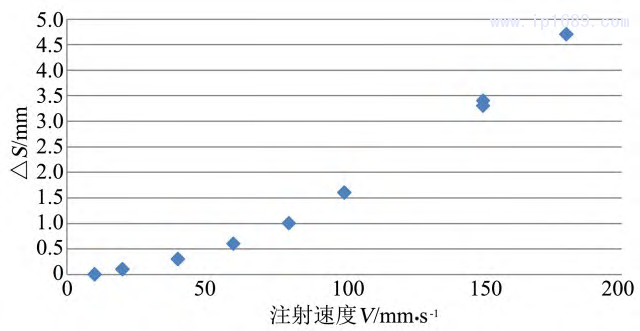
图2 V/P 切换位置波动幅度与注射速度散点图
3.2 试验数据变换
△S与V的原始数据集中,速度V的值分布在0~200mm/s,而△S的值域为0~5mm,为使2组变量的数值尽量接近,需要对变量V进行数据变换。任何注塑机都有一个标定的注射速度最大值,因此任意速度V都可以表示注塑机最大速度的百分比,将其映射到0~1的区间,得到新的变量V',定义V'为注射速度系数。该试验对象的注塑机最大注射速度为200mm/s
3.3 试验数据拟合
由于任一函数都可以用多项式逼近,多项式回归有广泛的应用,尤其在误差补偿方面已有大量的研究报道。杜西亮等[7]利用多项式拟合智能传感器的非线性补偿方程,王智明等[8]根据多项式回归理论,建立了机床热误差补偿模型。试验数据涉及的注射速度和V/P切换位置误差2个变量也可以通过构建一元多项式来拟合。
多项式回归公式为:
构建多项式函数需求解a0、a1、a2……am,其中m为多项式的项数,以数组x[1,2,3]和y[1,3,9]为例,计算其拟合二项式y=a0+a1x+a2x2的各项系数时,首先需根据正规方程组矩阵构建三行三列的数据矩阵X。
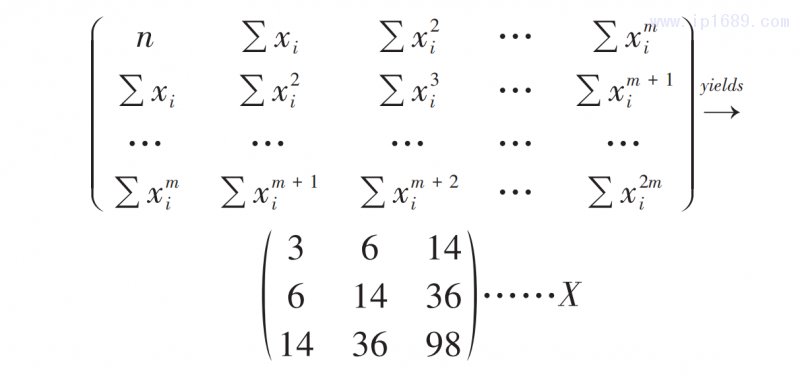
正规方程组矩阵中n是x数组中所有项0次方的加和∑x0i,其值等于x数组中项的数量。
再根据求偏导数矩阵,计算x数组中每一项的0~2次方与y数组中对应各项的乘积再加和,构建一个三行一列数据矩阵Y。
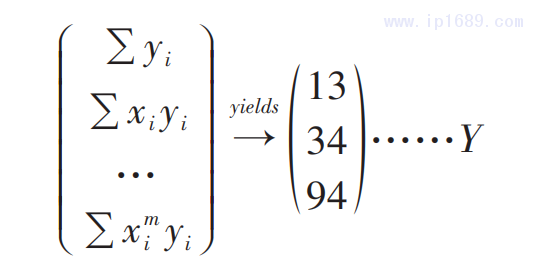
最后将X和Y代入多项式的矩阵公式中:

变换得到关于a0、a1、a2的三元一次方程组
求解上述方程组可知a0=3,a1=-4,a2=2,得到数组x[1,2,3]和数组y[1,3,9]的二次项式拟合方程为:y=3-4x+2x2。
在实际操作中,可以通过Matlab、CurveFitter等软件快速拟合一组数据的多项式拟合方程,图3所示展示了利用Excel的回归分析工具拟合试验变化数据集的2~6项拟合多项式。
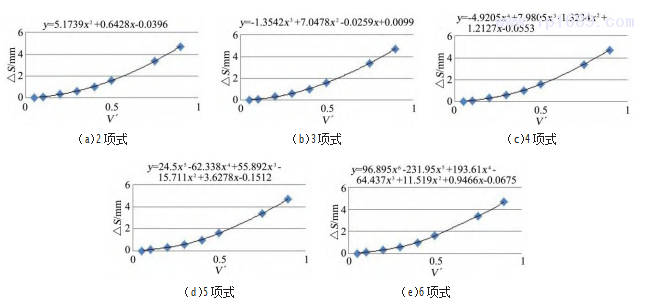
图3 试验数据的多项式拟合方程
根据上述5个拟合方程分别计算各个V'下的△S',通过比较位置偏差实际值△S与拟合方程计算值△S'的差异来评价其拟合效果。
误差比较法显示,多项式方程的项数越高,其拟合误差越小,但另一方面随着项数的增加,方程变得更加倾向于拟合所得到的数据点,导致过拟合的情况急剧增大。由于变量V'代表的是注塑机的注射速度,其大小是有限度的,可以将图3所示的方程曲线前推一个周期,通过观察各自的单调性来确定试验数据最合适的拟合方程项数。
显示变量V'前推一个周期后,4、5、6项式的方程曲线有明显的变形,如图4所示,可以预见在有限的范围内,V'增加到一定程度后,其预测结果将发生明显的偏差,因此4、5、6项式方程对研究的试验数据存在明显的过拟合问题。
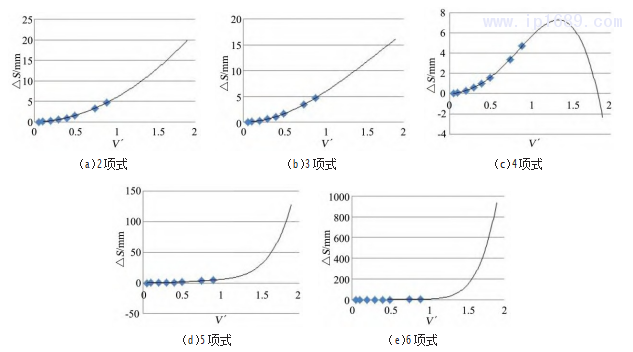
图4 多项式拟合方程曲线前推一个周期
3.4 试验结果
综合以上分析,确定试验注塑机V/P切换位置控制偏差与注射速度的函数关系方程为△S=0.0099-0.0259V'+7.0478V'2-1.3542V'3
该方程预测平均偏差仅0.02mm,适用于该注塑机标定最大注射速度2倍以内的任意速度,具有较高的精度和稳定性。
4 结束语
V/P切换位置是影响成型制品质量的一个关键参数,合理的切换位置可以避免或减轻短射、飞边、困气、残余应力等注射缺陷。试模时,工艺人员需要进行一系列欠注试验,通过观察欠注样件的充填状态确定V/P切换位置,而工艺优化过程伴随着注射速度的调整。由于电机传动系统过渡惯性的存在,导致随着注射速度的每一次改变,都需要重新进行V/P切换位置的调试,提高了试模成本。针对电动注塑机多个速度级别下对应切换位置的波动量进行多项式回归分析,构建了V/P切换位置控制误差△S和注射速度系数V'的三项式回归方程,实现对注塑机V/P控制偏差的预测。鉴于多项式回归法的广泛适应性以及注塑机注射速度的极值特定性,理论上任何注塑机的V/P控制波动量均可以用其注射速度的多项式函数表达。
对注塑机V/P控制波动进行函数化表达可以有效补偿其控制误差,同时结合注射仿真分析技术,实施以目标导向的工艺优化,改进试模过程,提高试模效率,促进企业的技术发展和效益提升。另一方面随着相关研究的不断拓展和深入,更多关于注塑机控制误差的算法将被开发,如速度、压力、开合模、推出等方面,用于优化和改进控制系统,实现注塑机控制稳定性的全方位提升。
参考文献:
[1]刘子恒.我国注塑机控制技术及发展趋势[J].中国包装工业,2011(3):46,48.
[2]刘立柱.新型双色注塑机液压系统高动态稳定性的研究[D].北京:北京化工大学,2016:38-39.
[3]康存锋,刘鑫,马春敏,等.全电子注塑机的合模控制及锁模力的研究[J].工程塑料应用,2009,37(1):71-74.
[4]董召然.注塑机注射速度和保压压力控制及注射保压切换方法研究[D].沈阳:东北大学,2008:50-52.
[5]唐杰,黄荣学,王全亮,等.CAE技术在汽车灯罩设计中的应用[J].模具工业,2020,46(3):12-17.
[6]王策,吴中旺,赖兴华,等.动力电池盖板下绝缘塑胶的模流分析与工艺优化[C].重庆:国际汽车交通安全学术会议,2018:180-185.
[7]杜西亮,孙慧明.多项式回归在智能传感器线性化中的应用[J].传感技术学报,2005,18(1):212-214.
[8]王智明,彭安华,王其兵.多项式回归理论在机床热误差建模中的应用[J].兰州理工大学学报,2007,33(6):40-42.












 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...














